(2: 水利部淮河水利委员会, 蚌埠 233001)
(2: The Huaihe River Commission of the Ministry of Water Resources, P. R. C, Bengbu 233001, P. R. China)
湖泊是重要的国土资源,具有调节河川径流、提供农业、工业和生活用水、繁衍水生生物、改善区域生态环境等多种功能.我国湖泊众多,共有24800多个,其中面积在1 km2以上的天然湖泊就有2693个[1],主要分布在东部平原和青藏高原地区.湖泊及其流域是人类赖以生存和发展的重要场所,然而由于经济的快速发展,闸坝建设、围湖造田、生产生活的过度取水以及不节制地向水体排放污染物等行为已经严重影响了湖泊生态环境,其中水位变化已经危害了湖泊生态系统健康,对湖泊生物多样性,湖泊结构、功能完整性造成了威胁.
然而,国内外对生态需水的研究主要集中在河流方面,对河流来说,最小生态流量是其生存警戒线.针对河流生态流量计算的研究也十分成熟,目前全球约有200多种河流生态流量的计算方法[2],依据不同的资料和不同的保护目标,主要可分为水文学方法(Tennant法、Texas法、基本流量法、RVA法等)、水力学方法(湿周法、R2-CROSS法、华盛顿方法等)、生物栖息地模拟法(IFIM法、流量事件法、鱼类生境法、生物空间最小需求法等)、整体法(BBM法、DRIFT法、HEA法等)及其它方法.
对于湖泊生态需水的研究开始于20世纪末,Raskin等[3]提出,为了保证水资源的可持续利用,应首先满足湖泊生态系统对水量的需求;Baird等[4]针对湖泊的结构和功能,分析了水生植物与水文过程之间密切的关系,强调了水对自然保护和生态恢复所起到的作用.我国对湖泊生态需水的研究主要集中在21世纪初,依据所保护的敏感指示物种对水环境指标的要求来进行计算[5]:刘静玲等[6]根据湖泊的基本特征提出了湖泊生态需水量的不同计算方法和相应指标体系,主要有水量平衡法、换水周期法、最小水位法和功能法;徐志侠等[7]根据水文循环原理,将吞吐型湖泊生态需水分为入湖生态需水、湖区生态需水和出湖生态需水3个部分,并提出了吞吐型湖泊最小生态需水计算模型,将其运用于南四湖生态需水的计算[8];崔保山等[8]从生态水文学原理出发,对湖泊最小生态需水量的概念进行了探讨,并提出了计算最小生态需水量的3种方法:曲线相关法、功能法和最低生态水位法.此后,不同学者根据所研究湖泊的特点,运用这些方法及其改进的方法对全国各大湖泊的生态需水和生态水位进行了计算.
由上可以看出,国内外对于湖泊生态需水的研究主要集中在水量和水位上,其中水位的变化更能直观的体现湖泊水量的变化,以水位作为标准和依据也便于对湖泊水量进行调控,而生态水位则是湖泊水资源开发的红线,是必须保证的,在此水位以上,湖泊中的物种和群落才可以正常生存、繁衍和演替,生态系统的结构和功能才可以得到维系[10].但对于湖泊生态水位的计算,目前的方法大多求到的都是一个固定水位,但是却忽略了湖泊年内水位变化的过程,即湖泊动、植物在不同季节,不同生长阶段对水位有不同的要求.
高邮湖为全国第六大淡水湖,江苏省内第三大淡水湖,也是淮河的入江水道.从1980s初开始大规模发展围网养蟹,由于持续过度开发,湖泊自然生产力下降,加之近年来经济高速发展,水资源利用加大,给高邮湖生态需水带来了巨大压力[11].因此本文以高邮湖为研究对象对其水文过程进行分析,借鉴河流生态流量计算中的变异性范围法(RVA法),构建高低水位值、高低水位发生时间和持续时间6个指标,基于高邮湖天然水位变化特征给出生态水位目标值范围,并分析其生态水位年内、年际保障程度和保障规律,找到高邮湖生态水位的敏感时期,为湖泊水资源的合理开发和利用、流域水资源调度以及恢复湖泊水生生态系统的健康提供依据.
1 研究区域与数据来源高邮湖(32°42′~33°10′N,119°06′~119°25′E)位于江苏省中部高邮市(图 1),连接江苏、安徽两省,总面积760.67 km2.湖底平坦,湖底高程3.5~4.5 m,死水位5 m,死库容4.6×108 m3,属浅水湖泊.高邮湖湖水主要由地表径流补给,三河入湖水量占总入湖水量的95%以上,另由安徽境内的白塔、铜龙、秦楠、杨村和王桥等5条小河补给,最终由东南部高邮湖控制闸入长江.高邮湖地处北亚热带季风气候区,年均气温14.7℃,年均降水量1029 mm,蒸发量890 mm.
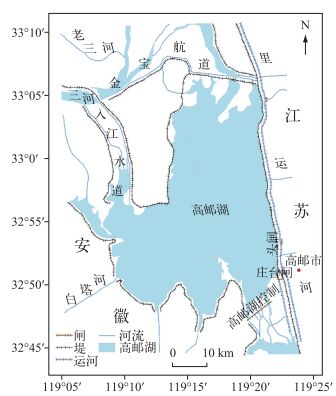
|
图 1 高邮湖地理位置 Fig.1 The geographical location of Lake Gaoyou |
高邮湖拥有丰富的生物资源,水生植物有53科131种,浅水湖滩产芦苇、菱、藕,动物122种,盛产青鱼、白鱼、黑鱼、鳊鱼、鲤鱼、鳗鱼等鱼类,尤以青河虾、银鱼、螃蟹闻名,湖面上有鸥、鹭、鹤以及野鸭等水鸟常出没于芦苇荡.
高邮湖周边土地利用情况如图 2所示.湖泊周围被耕地和城镇用地包围,受人类活动影响剧烈,开发利用程度高.本文采用高邮湖1953-2013年高邮站实测日水位数据和实测日降水数据进行水文过程的分析和生态水位的计算.
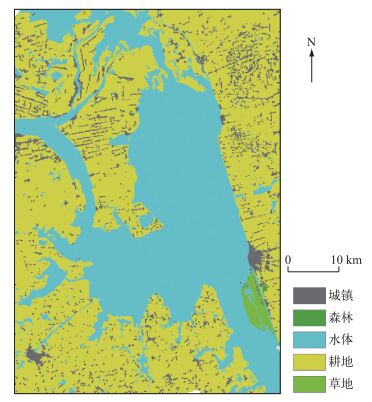
|
图 2 高邮湖周围土地利用类型 Fig.2 Land use types surrounding Lake Gaoyou |
湖泊生态水位是指维持湖泊生态系统结构、功能的完整性,维持生物多样性的最低水位.在长期的生态演变中,湖泊生态系统已经适应了湖泊水位的扰动,因此可以以天然情况下的低水位或选择一定保证率下的天然水位作为湖泊最低生态水位[8].
由于生态水位的计算要求天然水位,而本研究只有高邮湖实测水位资料,且进行天然序列还原计算相当困难.本文认为水文序列发生变化是由于气候变化和人类活动的因素造成的,而湖泊生态系统适应变化前的水位,找到水文序列的突变点以该点对序列进行分割,突变点之前的水位序列则可近似认为是天然状况下的水位序列.所以本文首先利用滑动T法和M-K法对高邮湖实测水位序列(1953-2013年)进行突变检验,将突变前的序列用于生态水位计算,突变后的序列用于分析人类活动影响后生态水位的保障情况.
2.1 最低生态水位计算在进行突变检验的基础上,本文分析了突变前的水位变化过程,以湖区主要动植物为保护目标,利用最低生态水位法中的年保证率法计算高邮湖最低生态水位,并结合年内展布法进行逐月的展布.
2.1.1 年保证率法基于计算河道需水量的月保证率设定法的基本原理,结合水文学方法中的最枯月均流量法来计算湖泊最低生态水位,计算方法为:
| ${h_{\min }}{\rm{ = }}\mu \cdot \bar h$ | (1) |
式中,hmin为最低生态水位,h为设定保证率下对应的水文年年均水位,μ为权重.
具体步骤为:根据水位序列,将历年最低水位按从大到小的顺序进行排列,根据湖泊自然地理、结构和功能选择适宜的保证率,计算该保证率所对应的水文年年均水位,最后根据水文年湖泊生态系统健康等级来估算μ值[12],生态系统越健康,μ值越小.湖泊生态系统健康等级分别为优、较好、中等、差和极差, 对应μ值分别为0.945、0.975、1.000、1.005和1.013.
2.1.2 年内展布法将所计算出的hmin与多年年均水位H之比作为同期均值比η,并以多年月均水位过程
| $\eta = {h_{\min }}/\bar H,其中\bar H = \frac{1}{{12}}\sum\limits_{i = 1}^{12} {\overline {{h_i}} ,\overline {{h_i}} = \frac{1}{n}} \sum\limits_{j = 1}^n {{h_{ij}}}$ | (2) |
式中,
| ${h_{{\rm{e}}i}} = {{\bar h}_i} \cdot \eta $ | (3) |
生态水位并非一个恒定值,而是一个数值区间,包含了水位变动的范围、频率、发生时间、持续时间及其他规律性等重要信息[10],所以本文借鉴河流生态流量计算中的变异性范围法(RVA法),构建高低水位值、高低水位发生时间和持续时间的指标,基于高邮湖天然水位变化特征给出生态水位目标值范围.
RVA法是Richter在1997年提出的一种评估河流生态水文变化的指标体系,该方法是在IHA(Indicators of Hydrologic Alteration)法[14]的基础上,依据河流系列长度大于20年的日水文资料,从流量大小、时间、频率、历时和变化5个方面构建了33个具有生态意义的关键水文参数值[15],在河流生态流量计算、水利工程对水文过程影响等方面已有广泛的应用:李兴拼等[16]以RVA法评估枫树坝水库建成后对东江上游河川径流特性的影响;盛杰等[17]应用RVA法对嫩江干流尼尔基水库下游河道生态需水以及水库现行调度方案运行对河流生态水文过程的影响进行了分析,建立了生态调度模型并提出该工程调度的优化建议;孙照东等[18]采用RVA法建立了引水枢纽调度模型,以维持引水枢纽以下河道生态完整性为水资源管理目标,估算了大通河的可外调水量.而湖泊水位与河流流量有相似的变化过程,却很少有人研究其变化规律,将RVA法其中的部分指标借鉴于湖泊生态水位变化的计算当中,能较好地分析湖泊年内的高、低水位变化情况,有利于湖泊的生态保护.
2.2.1 水位指标RVA法中高水位指长系列日水位频率低于25%的水位,低水位指长系列日水位频率高于75%的水位[19],湖泊高、低水位计算公式分别为:
| $Hh = {P_{25\% }}\left( {{h_i}} \right)$ | (4) |
| $Lh = {P_{75\% }}\left( {{h_i}} \right)$ | (5) |
式中,Hh、Lh分别为高水位(m)和低水位(m), P25%(hi)和P75%(hi)分别为25%和75%保证率下的湖泊日水位(m).
2.2.2 发生时间指标高水位发生时间(月份)为月均水位初次大于高水位的月份,低水位发生时间(月份)为当年高水位结束后月均水位初次小于低水位的月份,这个日期可能处于当年的后半年,也可能处于次年的上半年,计算公式分别为:
| $H{h_{{\rm{st}}}} = {\rm{min}}\left( i \right),s.t.\frac{1}{n}\sum\limits_{j = 1}^n {{h_{ij}} \ge Hh} (i = 1,2, \cdots ,12)$ | (6) |
| $L{h_{{\rm{st}}}} = {\rm{min}}\left( i \right),s.t.\frac{1}{n}\sum\limits_{j = 1}^n {{h_{ij}} \le Lh} \left( {i = 7,8, \cdots ,12,次年1,2, \cdots ,6} \right)$ | (7) |
式中,Hhst和Lhst分别为高水位发生时间和低水位发生时间(月份);hij为第i月第j日的湖泊日水位(m);n为第i月的天数.
2.2.3 水位历时指标水位历时是指高、低水位发生的持续时间,可由其结束时间减去其发生时间而得,高水位结束时间是指当年月均水位最后一次大于高水位的时间(月份),低水位结束时间是值月均水位最后一次小于低水位的时间(月份),该时间有可能发生在当年下半年,也有可能在次年上半年.具体计算公式如下:
| $H{h_{\rm{d}}} = H{h_{{\rm{et}}}} - H{h_{{\rm{st}}}}$ | (8) |
| $H{h_{{\rm{et}}}} = {\rm{max}}\left( i \right),s.t.\frac{1}{n}\sum\limits_{j = 1}^n {{h_{ij}} \ge Hh} {\rm{ }}\left( {i = 1,2, \cdots ,12} \right)$ | (9) |
| $L{h_{\rm{d}}} = L{h_{{\rm{et}}}} - L{h_{{\rm{st}}}}$ | (10) |
| $L{h_{{\rm{et}}}} = {\rm{max}}\left( i \right),{\rm{ }}s.t.{\rm{ }}\frac{1}{n}\sum\limits_{j = 1}^n {{h_{ij}} \le Lh} \left( {i = 7,8, \cdots ,12,次年1,2, \cdots ,6} \right)$ | (11) |
式中,Hhd和Lhd分别为高水位和低水位的持续时间,Hhet和Lhet分别为高水位和低水位的结束时间(月份),n为第i月的天数.
2.3 保障程度计算关于河道内生态流量保障程度的定义有很多,但总体大致分为2种:第一种为实际径流量与生态流量的比值[20];第二种以实际流量大于生态流量的历时占序列总历时的比值[21].本文借鉴潘扎荣等[22]对生态流量保障程度的定义,将湖泊生态水位保障程度定义为在一定时期内,湖泊实测水位大于生态水位的序列长度与总序列长度的比值.计算公式如下:
| ${E_N}{\rm{ = }}\frac{{\sum\limits_{k = 1}^N {Sgn\left( {{h_{\rm{k}}} - {h_{\rm{e}}}} \right)} }}{N} \times 100{\rm{\% }},Sgn\left( {{h_{\rm{k}}} - {h_{\rm{e}}}} \right){\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {1,} & {若{h_{\rm{k}}} - {h_{\rm{e}}} \ge 0}\\ {0,} & {若{h_{\rm{k}}} - {h_{\rm{e}}} < 0} \end{array}} \right.$ | (12) |
式中,EN是N日的日生态水位保障程度(%),N为统计天数,he和hk分别是生态水位(m)和实测水位(m).则第i月多年生态水位保障程度Ei及第j年年度生态水位保障程度Ej计算公式分别为:
| ${E_i}{\rm{ = }}\frac{{\sum\limits_j^n {\sum\limits_{k = 1}^I {Sgn\left( {{h_{jik}} - {h_{{\rm{e}}i}}} \right)} } }}{n} \times 100{\rm{\% }},Sgn\left( {{h_{jik}} - {h_{{\rm{e}}i}}} \right){\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {1,} & {若{h_{jik}} - {h_{{\rm{e}}i}} \ge 0}\\ {0,} & {若{h_{jik}} - {h_{{\rm{e}}i}} < 0} \end{array}} \right.$ | (13) |
式中,Ei为第i月的多年生态水位保障程度(%),hjik为第j年第i月第k日的实测水位(m),n为统计年份数,I为i月的天数.
| ${E_j}{\rm{ = }}\frac{{\sum\limits_{i = 1}^{12} {\sum\limits_{k = 1}^I {Sgn\left( {{h_{jik}} - {h_{{\rm{e}}i}}} \right)} } }}{{{M_j}}} \times 100{\rm{\% }},Sgn\left( {{h_{jik}} - {h_{{\rm{e}}i}}} \right){\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {1,} & {若{h_{jik}} - {h_{{\rm{e}}i}} \ge 0}\\ {0,} & {若{h_{jik}} - {h_{{\rm{e}}i}} < 0} \end{array}} \right.$ | (14) |
式中,Ej为第j年的年度生态水位保障程度(%),Mj为j年的天数.
3 结果与讨论 3.1 高邮湖水位变异点研究采取高邮湖61年(1953-2013年)的年均水位资料,M-K和滑动T检验显著性水位都选取α=0.05进行突变点的检验,检验结果如图 3所示.

|
图 3 高邮湖1953-2013年年水位M-K法(a)和滑动T法(b)检验 Fig.3 Annual average water level of Lake Gaoyou was tested by Mann-Kendall test method(a) and moving T test method(b) during 1953-2013 |
通过M-K检验,UF和UB统计量有两个交点分别发生在1996年和1997年,说明高邮湖年水位在1996和1997年发生了突变,年水位过程1953-1998年呈上升趋势,且在1953-1978年上升趋势明显;2000-2010年呈下降趋势,2010年以后又呈上升趋势(图 3a).通过滑动T检验,高邮湖年水位在1997、2001、2002年都发生突变(图 3b).
由于检验方法的不同,两种检验的结果略有偏差,但结果均表明高邮湖年水位在1997年附近发生了突变.高邮湖最大年均水位为6.61 m,出现在2003年,最小年均水位为4.92 m,出现在1978年,多年年均水位为5.80 m,突变前多年平均水位为5.72 m,突变后多年平均水位为6.00 m(图 4a).

|
图 4 高邮湖1953-2013年均水位(a)和年降水量(b)变化 Fig.4 Annual water level process(a)and precipitation(b)of Lake Gaoyou during 1953-2013 |
通过年降水量5年滑动平均可以看出,高邮湖降水过程在突变点1997年前后变化不大,多年平均降水量1029 mm,1955-1996年多年平均降水量1034 mm,1997-2013年多年平均降水量1019 mm,仅相差15 mm(图 4b),属于正常波动范围以内,所以本文认为高邮湖水位发生突变不是气候变化导致的,而是由于人类活动的影响.
虽然检验所得突变发生在1997年,但人类活动对湖泊水位突变的影响是一个长期的结果,且高邮湖属于淮河流域,淮河上游来水对高邮湖水位有很大影响,根据《淮河流域综合规划》,淮河流域1990s开始以治淮19项骨干工程为重点,开展新一轮治淮建设,认为这些工程建设可能对淮河流域天然径流产生了影响,导致高邮湖水位序列的突变.所以,本文选取1953-1992年40 a水位资料近似认为天然状况下的水位序列计算高邮湖高、低水位值和生态水位,以1993-2013年21 a水位资料分析高邮湖生态水位保证程度.
3.2 高邮湖天然水位特征利用高邮湖1953-1992年40 a的日水位序列求逐日的多年平均值、多年最高值和多年最低值(图 5).高邮湖水位年内总体呈单峰分布,全年以8月为界,1-6月底水位平缓,基本保持不变,7月初-8月上旬水位呈上升趋势,8月中旬-12月底缓慢下降.多年平均水位变化约1 m左右,年内水位变化不大,多年日最高水位变化约3.5 m,多年日最低水位变化约0.8 m,同一天的最高和最低水位差最大能达到5 m.根据公式(4)~(5),高邮湖高水位,即25%保证率水位为5.91 m,低水位即75%保证率水位为5.33 m.总体上,高邮湖水位呈现出汛期(6-9月)水位高、非汛期(10次年3月)水位低的年内变化特征.
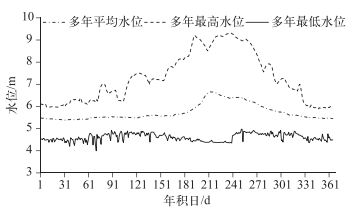
|
图 5 高邮湖1953-1992年日水位变化 Fig.5 The daily mean multi-year water level process of Lake Gaoyou during 1953-1992 |
由高邮湖1953-1992年的日水位序列,根据年保证率法,计算逐年最低水位,选择50%保证率最低水位所对应的水文年的年均水位作为h,根据高邮湖的健康评价等级为中等[23-24],对应μ值取1,得到高邮湖年均生态水位为5.37 m.再计算出高邮湖多年年均水位为5.71 m,由生态水位与多年年均水位的比值得到同期均值比η为0.94,再根据多年月均过程进行年内分配,得到高邮湖1-12月逐月最低生态水位分别为5.08、5.07、5.15、5.15、5.20、5.27、5.75、6.09、5.85、5.46、5.23和5.12 m.
根据实地调查,高邮湖主要植物群落为:金鱼藻群落(沉水植物)、芦苇群落(挺水植物)和野菱群落(浮叶植物),以高邮湖生态系统中的鱼类和植物生长、繁衍对水深的需求作为检验生态水位计算的一个标准,不同的水生和陆生植物有不同的适宜水生,而沉水植物和挺水植物更易受到水位高低的影响[25].根据相关资料[26],得到沉水植物的适宜水深为60~200 cm,挺水植物的适宜水深为-30~-50 cm(负值表示水面以上),高邮湖湖底高程为3.5~4.5 m,生态水位为5.07~6.09 m,可以看出最低生态水位是符合植被生长的要求的.而野生鱼类生存和繁殖的最小水深为1 m[27],最低生态水位也满足鱼类产卵、育幼和生存的需求,所以认为本次对高邮湖最低生态水位的计算能符合鱼类和植物生存要求.
做高邮湖最低生态水位年内变化过程曲线,高邮湖年内最低生态水位变化过程与其水位过程有相同的趋势,冬、春季生态水位低,夏、秋季生态水位高,其中2月生态水位最低,为5.07 m,8月生态水位最高,为6.09 m,年内生态水位差最大为1.02 m. 8月最低生态水位高于计算的高水位,11月-次年6月的最低生态水位低于计算的低水位(图 6).本文认为,在高水位时期,湖泊水位在保障其高水位天数的同时不能低于其最低生态水位;在低水位时期,湖泊水位也应该在不低于最低生态水位的同时保障其低于低水位的天数,所以本文对高、低水位的开始时间和历时进行进一步的计算和分析.
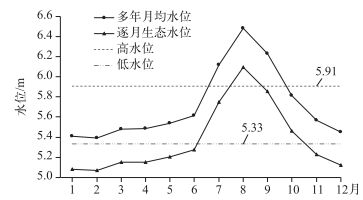
|
图 6 高邮湖逐月生态水位过程 Fig.6 Monthly process of ecological water level of Lake Gaoyou |
水位的周期性变动可显著影响湖滨带植物群落的组成与分布[28].冬、春季挺水植物冬眠,保持较低的水位可以给植物种子和繁殖体的萌发提供充足的光照和氧气;夏季是湖滨带挺水植物生长的旺季,高水位可以促进挺水植物的快速生长,而夏季的低水位会使水温和盐度上升,陆生生态系统向湖中心移动,浅水湖泊可能会逐渐沼泽化[29].形成冬低夏高的水位波动模式,对水生植物的生长、发育是有利的.基于高邮湖1953-1992年的日水位数据,采用公式(6)~公式(11),计算出高邮湖高水位和低水位每年发生的时间和历时(图 7).
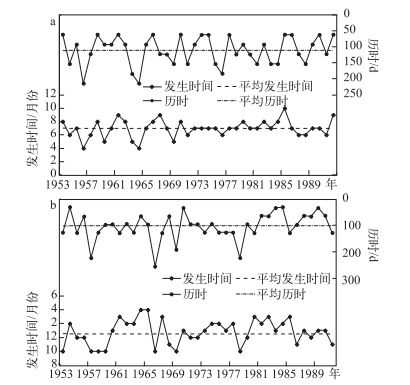
|
图 7 高邮湖1953-1992年高水位(a)和低水位(b)发生时间与历时 Fig.7 The start time and duration period of high water level(a) and low water level(b) of Lake Gaoyou during 1953-1992 |
根据高邮湖每年高、低水位的开始时间、历时及降水过程,将每年的水位过程划分为3个时期(表 1):高水位时期(7-10月),水位在5.91 m以上的天数需达到111 d左右;低水位时期(12-次年3月),水位在5.33 m以下的天数需达到96 d左右;其余月份为高低水位间的过渡时期,水位一般介于高、低水位之间.
| 表 1 高邮湖年内生态水位过程 Tab.1 The ecological water level process of Lake Gaoyou in a year |
根据高、低水位时期划分求出生态水位在此期间的均值,高邮湖在高水位时期最低生态水位均值为5.79 m,低水位时期最低生态水位均值为5.11 m,过渡时期的最低生态水位为5.21 m.
3.5 高邮湖生态水位保障程度根据高邮湖生态水位过程要求,利用公式(13)~公式(14)分析1993-2013年逐日实测水位的年内和年际保障程度,并研究其高、低水位保障情况.
由计算结果绘制高邮湖逐日生态水位保障程度年内变化及年际变化过程可以看出(图 8),高邮湖高水位时期(7-10月)生态水位高但生态水位保障程度低,只有70%左右,其中7月保障程度最低,为60.83%;低水位时期及过渡时期生态水位保障程度较高,能达到90%左右.可以得出,夏季高水位时期是生态水量的枯水期,主要原因有:夏季大量湖泊蓄水用于农作物灌溉;夏季气温较高,蒸发较大;由于淮河流域洪水灾害严重,高邮湖作为其中一个蓄洪区,提前降低湖泊水位以满足防洪需求.
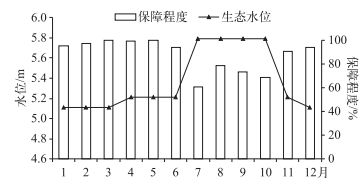
|
图 8 高邮湖逐月生态水位及多年月保障程度 Fig.8 Ecological water level and its monthly assuring degree process of Lake Gaoyou |
高邮湖生态水位年际变化较大,其中1995-2000年呈现出逐渐上升的趋势,在2001年有一个急剧的下降,2002-2012年一直保持在较高水平,在2013年略有降低(图 9). 21年来生态水位保障程度最低发生在1994年,为49.59%,其次为2001年,为50.41%.生态水位的保障情况与当年的丰、枯情况有关,但自2002年后保障程度明显好转,说明随着淮河上、中游水利工程的逐渐完善,闸、坝、水库的调蓄作用对高邮湖生态水位的保障是有一定促进作用的.

|
图 9 高邮湖逐年保障程度 Fig.9 Annual assuring degree process of ecological water level of Lake Gaoyou |
从1993-2013年高邮湖高、低水位的保障情况上看(表 2),1993-2001年高水位的保障程度不高,常出现全年水位都达不到高水位或只有1、2个月水位在高水位以上的情况;2002年以后高水位都能得到很好的满足,高水位历时甚至远大于其需要的天数,遇到丰水年(2003年)全年水位都在高水位之上.但低水位的保障程度很差,除1994和2001年外,其余19年低水位的保障情况都为0,说明高邮湖水位长期处于高水位状态,原因可能是高邮湖出湖水量由水闸控制,低水位时期为了保证充足的水位以满足鱼、虾、蟹养殖的需求将水闸关闭,导致湖泊水位没有自然降低,这虽然有利于经济发展却违背了湖泊自然的高、低水位变化规律,对湖泊生态系统的健康极为不利.
| 表 2 1993-2013年高、低水位保障情况 Tab.2 Assuring degree of high water level and low water lever during 1993-2013 |
水位的周期性变动有利于湖滨植物群落的发育,长期的高水位和非周期性季节变化会破坏生态系统长期以来对水位周期性变化产生的适应性,冬春季节的高水位使沉水植物和挺水植物种子的萌发和生长缺少光照和氧气,抑制湖内、湖滨带植物的生长,使湖泊生态系统的生产力和物种多样性降低.所以应该在满足高水位时期生态水位的同时,在保障高邮湖防洪抗旱功能和提供生产、生活用水的前提下,在低水位时期适当开闸放水,对恢复高邮湖的生态环境具有促进作用.
4 结论本文利用M-K法和滑动T法对高邮湖1953-2013年的年均水位进行突变检验,分析了高邮湖1953-1992年来水文变化规律,以湖区主要动植物为保护目标,利用最低生态水位法中的年保证率法计算高邮湖最低生态水位,结合年内展布法得到逐月最低生态水位过程,并借鉴河流生态流量计算中的变异性范围法(RVA),构建高低水位值、高低水位发生时间和持续时间的指标,计算出湖泊高、低水位发生时间及历时,并对其生态水位及其高低水位保障程度进行分析计.具体结论有:
1) 高邮湖年水位在1997年附近发生了突变,选择1953-1992年水位资料近似认为为天然状况下的水位序列计算高邮湖高、低水位值和生态水位,利用1993-2013年逐日实测水位分析生态水位年内和年际保障程度.
2) 根据多年日水位计算,将高邮湖每年的水位过程划分为3个时期:高水位时期(7-10月),水位在5.9 m以上的天数需大于111 d,且该时期最低生态水位为5.8 m;低水位时期(12-次年3月),水位在5.33 m以下的天数需达到96 d左右,且该时期最低生态水位为5.1 m;其余月份为高低水位间的过渡时期,水位一般介于高、低水位之间,最低生态水位为5.2 m.
3) 从生态水位保障程度的年内过程来看,高邮湖高水位时期生态水位保障程度较低,最低发生在7月,为60.83%,年际生态水位保障程度变化较大,其中1994和2001年最低,分别为49.59%和50.41%,自2002年以后生态水位保障程度一直保持在较高水平.从高、低水位保障程度上看,高水位历时过长,而低水位天数远得不到保障,说明高邮湖一直处于较高水位状态,这违背了湖泊自然的高、低水位变化规律,对湖泊生态系统健康极其不利.
湖泊在长期的发育过程中已经形成了适宜的水位变化规律,而人类活动对湖泊水位的改变已经严重影响了湖泊生态系统的健康,高水位时期为了防洪、灌溉的需求使其最低生态水位无法保障,低水位时期为了鱼、虾、蟹的养殖使水位长期保持在较高水位,虽然有利于经济发展却危害了湖泊生态系统的健康.为了减轻洪涝灾害淮河流域各水系受到水利工程高度控制,但在以后的发展过程中,人类应该加强重视河道、湖泊的自然过程,在保障高邮湖防洪抗旱功能和提供生产、生活用水的前提下,逐步恢复其生态系统自然的健康状态.
| [1] |
Ma Ronghua, Yang Guishan, Duan Hongtao et al. China's lakes at present:Number, area and spatial distribution. Sci China:Earth Sci, 2011, 41(3): 394-401. [马荣华, 杨桂山, 段洪涛等. 中国湖泊的数量、面积与空间分布. 中国科学:地球科学, 2011, 41(3): 394-401.] |
| [2] |
Tharme RE. A global perspective on environmental flow assessment:Emerging trends in the development and application of environmental flow methodologies for rivers. River Research and Applications, 2003, 19(5/6): 397-441. |
| [3] |
Raskin PD, Hansen E, Margolis RM. Water and sustainability. Natural Resources Forum, 1996, 20(1): 1-15. DOI:10.1111/narf.1996.20.issue-1 |
| [4] |
Baird AJ, Wilby RL. Eco-hydrology:Plants and water in terrestrial and aquatic environments. London: Psychology Press, 1999.
|
| [5] |
Jiang Dejuan, Wang Huixiao. Research advance in ecological and environmental water requirement. Chinese Journal of Applied Ecology, 2004, 15(7): 1271-1275. [姜德娟, 王会肖. 生态环境需水量研究进展. 应用生态学报, 2004, 15(7): 1271-1275.] |
| [6] |
Liu Jingling, Yang Zhifeng. A study on the calculation methods of the minimum eco-environmental water demand for lakes. Journal of Natural Resources, 2002, 17(5): 604-609. [刘静玲, 杨志峰. 湖泊生态环境需水量计算方法研究. 自然资源学报, 2002, 17(5): 604-609. DOI:10.11849/zrzyxb.2002.05.011] |
| [7] |
Xu Zhixia, Wang Hao, Tang Kewang et al. Minimum ecological water requirements for lakes taking in-sending out water. Resources Science, 2005, 27(3): 140-144. [徐志侠, 王浩, 唐克旺等. 吞吐型湖泊最小生态需水研究. 资源科学, 2005, 27(3): 140-144.] |
| [8] |
Xu Zhixia, Wang Hao, Dong Zengchuan et al. Minimum ecological water requirement for Nansi Lake. Journal of Hydraulic Engineering, 2006, 37(7): 784-788. [徐志侠, 王浩, 董增川等. 南四湖湖区最小生态需水研究. 水利学报, 2006, 37(7): 784-788.] |
| [9] |
Cui Baoshan, Zhao Xiang, Yang Zhifeng. Eco-hydrology-based calculation of the minimum ecological water requirement for lakes. Acta Ecologica Sinica, 2005, 25(7): 1788-1795. [崔保山, 赵翔, 杨志峰. 基于生态水文学原理的湖泊最小生态需水量计算. 生态学报, 2005, 25(7): 1788-1795.] |
| [10] |
De Emiliani MOG. Effects of water level fluctuations on phytoplankton in a river-floodplain lake system (Paraná River, Argentina). Hydrobiologia, 1997, 357(1/2/3): 1-15. |
| [11] |
Zhao Jianhua. The fishery present situation and development measures of Lake Gaoyou. Fishery Guide to be Rich, 2012(10): 19-20. [赵建华. 高邮湖区渔业的现状及发展措施. 渔业致富指南, 2012(10): 19-20.] |
| [12] |
Yang Zhifeng, Cui Baoshan, Liu Jingling. Theory, method and practice of environmental water requirement. Beijing: Science Press, 2003. [杨志峰, 崔保山, 刘静玲. 生态环境需水量理论, 方法与实践. 北京: 科学出版社, 2003.]
|
| [13] |
Pan Zharong, Ruan Xiaohong, Xu Jing. A new calculation method of instream basic ecological water demand. Journal of Hydraulic Engineering, 2013, 44(1): 119-126. [潘扎荣, 阮晓红, 徐静. 河道基本生态需水的年内展布计算法. 水利学报, 2013, 44(1): 119-126.] |
| [14] |
Richter BD, Baumgartner JV, Powell J et al. A method for assessing hydrologic alteration within ecosystems. Conservation Biology, 1996, 10(4): 1163-1174. DOI:10.1046/j.1523-1739.1996.10041163.x |
| [15] |
Shu Chang, Liu Suxia, Mo Xingguo et al. Estimation of instream ecological flow bases on RVA. Ecology and Environmental Sciences, 2010, 19(5): 1151-1155. [舒畅, 刘苏峡, 莫兴国等. 基于变异性范围法(RVA)的河流生态流量估算. 生态环境学报, 2010, 19(5): 1151-1155.] |
| [16] |
Li Xingpin, Huang Guoru, Jiang Tao. Evaluating alterations of runoff after Fenshuba reservoir construction based on RVA method. Water Resources and Power, 2009, 27(3): 18-21. [李兴拼, 黄国如, 江涛. RVA法评估枫树坝水库对径流的影响. 水电能源科学, 2009, 27(3): 18-21.] |
| [17] |
Sheng Jie, Guo Xuezhong, Chen Xiaoxia. Research on ecological reservoir reoperation based on RVA method. China Rural Water and Hydropower, 2012(6): 14-16. [盛杰, 郭学仲, 陈晓霞. 基于RVA法的水库生态调度研究. 中国农村水利水电, 2012(6): 14-16.] |
| [18] |
Sun Zhaodong, Shi Ruilan, Zheng Jianguo et al. Research on Datonghe River reoperation water on RVA method. Yellow River, 2009, 31(1): 51-52. [孙照东, 史瑞兰, 郑建国等. 基于RVA法的大通河可外调水量研究. 人民黄河, 2009, 31(1): 51-52.] |
| [19] |
Gan Feng, Tang Lin, Guo Huaicheng et al. New method and application of estimating ecological water level of the Lake Poyang. J Lake Sci, 2015, 27(5): 783-790. [淦峰, 唐琳, 郭怀成等. 湖泊生态水位计算新方法与应用. 湖泊科学, 2015, 27(5): 783-790. DOI:10.18307/2015.0504] |
| [20] |
Chen Ping, Cui Guangbai, Liu Zhengxiang. Setting up evaluation index system for the ecological river course in south China. Chinese Journal of Eco-Agriculture, 2007, 15(4): 166-169. [陈平, 崔广柏, 刘正祥. 南方生态河道评价指标体系初探. 中国生态农业学报, 2007, 15(4): 166-169.] |
| [21] |
Lin Mulong, Li Xiangyang, Yang Minghai. Probe into the index system for evaluating the health of the rivers in the Pearl River Basin. Pearl River, 2006(4): 1-3, 14. [林木隆, 李向阳, 杨明海. 珠江流域河流健康评价指标体系初探. 人民珠江, 2006(4): 1-3, 14.] |
| [22] |
Pan Zharong, Ruan Xiaohong. Spatio-temporal analysis of satisfactory degree of ecological water demand in Huaihe River Basin. Journal of Hydraulic Engineering, 2015, 46(3): 280-290. [潘扎荣, 阮晓红. 淮河流域河道内生态需水保障程度时空特征解析. 水利学报, 2015, 46(3): 280-290.] |
| [23] |
Li Can, Li Yong, Li Jia. Index system and methodology for health assessment of lakes. Sichuan Environment, 2011, 30(2): 71-75. [李灿, 李永, 李嘉. 湖泊健康评价指标体系及评价方法初探. 四川环境, 2011, 30(2): 71-75.] |
| [24] |
Fan Xu, Meng Lingfang, Liu Cui et al. Value assessment of ecological service function in Lake Gaoyou. Journal of Economics of Water Resources, 2015(1): 14-17. [樊旭, 孟灵芳, 刘翠等. 高邮湖生态服务功能价值评估. 水利经济, 2015(1): 14-17.] |
| [25] |
Liu Yong, Guo Huaicheng, Zhou Feng et al. Role of water level fluctuation on aquatic vegetation in lakes. Acta Ecologica Sinica, 2006, 26(9): 3117-3126. [刘永, 郭怀成, 周丰等. 湖泊水位变动对水生植被的影响机理及其调控方法. 生态学报, 2006, 26(9): 3117-3126.] |
| [26] |
Andrea JH. Implementation of a GIS to assess the effects of water level fluctuations on the wetland complex at Long Point, Ontario[Dissertation]. Waterloo:University of Waterloo, 2003.
|
| [27] |
Yu Danying, Jia Li. Study of ecological water level of Lake Hongze. Water Resources Planning and Design, 2006(2): 56-60. [郁丹英, 贾利. 关于洪泽湖生态水位的探讨. 水利规划与设计, 2006(2): 56-60.] |
| [28] |
Hill NM, Keddy PA, Wisheu IC. A hydrological model for predicting the effects of dams on the shoreline vegetation of lakes and reservoirs. Environmental Management, 1998, 22(5): 723-736. DOI:10.1007/s002679900142 |
| [29] |
Chen Changcai. A study of ecological water level requirement of Chaohu aquatic plant. China Rural Water and Hydropower, 2013(2): 4-7. [陈昌才. 巢湖水生植物对生态水位的需求研究. 中国农村水利水电, 2013(2): 4-7.] |
 2017, Vol. 29
2017, Vol. 29 

