(2: 苏州市气象局, 苏州 215131)
(2: Suzhou Meteorological Bureau, Suzhou 215131, P. R. China)
大型浅水湖泊(太湖)中,动力过程不仅对其营养盐的内源释放[1-2]、沉积物再悬浮、水体浊度变化[3-5]及藻类的水平输移[6]等有着重要作用,而且对湖泊环境的变化、湖泊生态系统的演替有着深远和复杂的影响[7].由此诸多学者对太湖流场、波流共同作用对底泥再悬浮及浊度等的时空演变进行了深入研究[8-10],揭示了太湖风生流、补偿流等湖流结构及其对底泥起悬和悬浮物沉降的影响规律.尽管该方面的研究取得了长足的进展,但多集中在悬浮物等水平输移、水平流场及其结构等方面,而基本忽略了强度较弱(通常较水平运动低一个或一个以上的量级)却控制物质、热量垂向分布、输移的次生垂向运动.由波浪破碎等动力作用和热力作用产生的次生垂向运动控制着水气界面及水体内部的物质、能量及动量的交换和输送[11],从而导致其成为影响水生生态系统演变的重要物理过程[12].
湍流是次生垂向运动的重要组成部分.其包含各种尺度的涡旋结构,具有宽泛的时间尺度和空间尺度、高度不稳定等特征;且涡旋的拉伸、形变等影响着三维湍流的演变,导致难以准确地定量描述各级湍流的产生、演变及消亡的规律.在描述湍流的参数中,湍流动能耗散率(ε)是度量湍流和混合程度的物理量[13]、闭合湍流动能方程的关键[14],也是模拟湖泊、海洋等水体动力学及生物化学过程的前提.近年随着声学多普勒流速剖面仪(Acoustic Doppler Current Profiles, ADCP)的应用,对海洋、近岸河口及海湾等处高频观测的三维流速研究取得了重要进展:基于能量波数谱在惯性子区间的特征,成功地推求了ε[15].水平流速切变和浮力作用导致的湍流各向异性可能对惯性子区间的波数范围造成影响,进而影响ε的计算误差[16-17];初步揭示了热力作用、波和流及其相互作用对ε廓线的影响特征[18-19];海底边界层中由流速切变产生的湍流动能与耗散通常呈现局地平衡[20].然而,关于ε的研究多数集中于海洋或深水湖泊,而针对大型浅水湖泊中湍流运动的研究却较为鲜见.
针对动力过程影响水生生态系统演变的研究中,秦伯强等[21]基于长期的野外观测和模拟实验提出了“适度”的湍流扰动促使蓝藻细胞通过碰撞形成的细胞团,更容易在水动力消失后快速上浮形成水华;Zhou等[22]通过实验证实“短时间尺度的湍流”(3天左右)有利于微囊藻的生长及其藻毒素的释放;在富营养化和春季温度偏高的前提下,流速、流量等动力作用是制约汉江硅藻水华的关键(敏感)因子[23-24].但有关内陆湖泊中湍流的生态效应及其定量影响机制方面的研究相对匮乏,基本仍处于“定性”的描述阶段.即使在流场数值模拟方面,涡旋粘性系数、湍流垂直扩散系数多假定为常数[8-10],从而导致降低了湖泊垂向运动的模拟精度,限制了对蓝藻水华形成机理的认识及水生生态环境修复的效果.
鉴于分层与混合中的湍流运动对大型浅水湖泊的垂向结构、物质和能量输送及水生生态系统演变的作用,因而迫切需要研究、分析大型浅水湖泊中ε的特征及其变化机制,为探究大型浅水湖泊的动力过程、水生生态系统中的物理、生物及化学过程的耦合效应奠定坚实的基础.以太湖为研究对象,利用ADCP和气象场等观测资料,探究大型浅水湖泊中ε的廓线特征,以期推动湖泊动力学及生态学相耦合的研究工作.
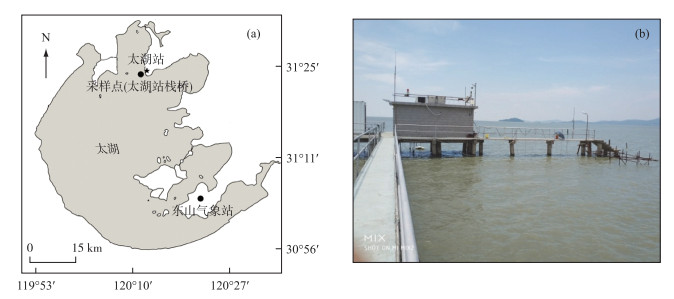
1 资料与方法 1.1 观测资料太湖是典型的大型浅水湖泊,面积为2338 km2,平均水深不超过2 m.为了能持续观测及保证供电条件,三维流速廓线、水温廓线及波浪的观测位置选择在中国科学院太湖湖泊生态系统研究站的栈桥(图 1).
|
图 1 中国科学院太湖湖泊生态系统研究站位置(a)及栈桥(b) Fig.1 Location (a) and trestle bridge (b) of Ecosystem Observation and Research Station in Lake Taihu, Chinese Academy of Sciences |
本文所用资料的观测时段为2017年10月29日02:00至2017年11月02日23:30.观测期间平均水深为2.3 m.观测数据说明及处理方法如下:
采用美国RoweTechnologies公司生产的ADCP(型号:Seaprofiler1200)高频测定水体的三维流速廓线.其工作原理如下:假定颗粒物的运动速度和水体流速一致,当发射的声波经颗粒物散射后导致其声学多普勒频移.基于此频移与水体流速的关系推算水体三维流速的廓线分布.与传统的流体流速测量方法相比,ADCP具有高分辨率,高精度等优点,尤其适用于复杂环境下流体流速的测量.高频观测(频率4 Hz)三维流速;观测层厚为0.1 m;观测开始深度为0.69 m;观测层数15层.针对原始三维流速数据,采用Turkey53H的方法[25]进行奇异值的确定、剔除及插补.
利用英国Valeport公司生产的方向波浪仪(型号:MIDAS)观测波高、波周期等参数,测定频率为8 Hz,每30 min采样4096次(约8 min左右),其观测结果为采样时段的统计值.
利用多个加拿大理查德布兰克研究公司(RBR)生产的水温仪(型号:TR1060),通过悬挂于不同深度测定水温廓线,深度间隔为10 cm,观测最大深度为1.9 m;时间间隔为10 min,即每隔10 min测定1次水温.
鉴于气象局的观测站点选址和业务观测相对规范,时间连续性和空间代表性较好;湖泊动力过程是大气对水体驱动作用在空间、时间上的累积效应的综合反映,而非局地(空间尺度)和瞬时(时间尺度)大气作用的体现.因而东山气象站(31.11°N,120.43°E,图 1)的观测数据更具有空间代表性,适用于探讨太湖水动力过程.本文采用苏州市东山气象站观测的风场(仪器型号:ZQZ-TF;安装高度10 m)、太阳短波辐射(仪器型号:WUSH-BRS;安装高度1.2 m)、气压(仪器型号:WUSH-TP300;安装高度1 m)、相对湿度(仪器型号:DHC2;安装高度1.5 m)、云量(定时人工观测)、气温(型号:WUSH-TW100;安装高度1.5 m)等数据.风场的观测频率均为逐小时,辐射数据频率为1 min.
1.2 方法 1.2.1 速度扰动量的分离鉴于湖流是波-流相互作用的综合体现,因而x、y、z方向的瞬时流速(u、v、w)包含雷诺平均速度(
| $ u=\overline{u}+\tilde{u}+u^{\prime} $ | (1) |
| $ v=\overline{v}+\tilde{v}+v^{\prime} $ | (2) |
| $ w=\overline{w}+\widetilde{w}+w^{\prime} $ | (3) |
其中:
| $ \overline{u}=\frac{1}{N} \sum\limits_{i=1}^{i=N} u_{i} $ | (4) |
| $ \overline{v}=\frac{1}{N} \sum\limits_{i=1}^{i=N} v_{i} $ | (5) |
| $ \overline{w}=\frac{1}{N} \sum\limits_{i=1}^{i=N} w_{i} $ | (6) |
式中,N是依据波浪仪在30 min内测定的瞬时速度次数.其中雷诺平均速度(
| $ <u>=\frac{1}{M} \sum\limits_{m=1}^{m=M} u(t+m \cdot T) $ | (7) |
波动轨迹速度产生于波浪作用,包含了波浪的周期信息,体现了对时间的依赖性,为位相平均速度与雷诺平均速度之差[26]:
| $ \tilde{u}= <u>-\overline{u} $ | (8) |
式中,T为波浪周期,m为波浪的周期数,M为确定位相速度的总周期数.为此可确定瞬时速度的扰动量(u′、v′、w′).
1.2.2 湍流动能耗散率的计算自然水体中的湍流动能主要来源于水平运动的垂直切变、波浪破碎、浮力及对流等动力过程,其中动能、势能(或波能)逐步衰减为各级湍涡,最终通过粘性效应耗散.可见,ε为单位时间内由于分子粘性作用耗散单位质量水体中湍流动能的能力[18].依据高频三维流速计算ε的过程如下:
利用傅里叶变换,将速度扰动量(u′、v′、w′)转换成频率域φ(k),k为波数,表达式如下:
| $ {S^2} = \overline {{{\left( {\frac{{{\rm{d}}\overrightarrow {\mathit{u'}} }}{{{\rm{d}}\mathit{z}}}} \right)}^2}} = \frac{1}{{\left( {{k_{\rm{U}}} - {k_{\rm{L}}}} \right)}}\int_{{k_{\rm{L}}}}^{{k_{\rm{U}}}} \varphi {(k)^2}{\rm{d}}k \approx \sum\limits_{{k_{\rm{L}}}}^{{k_{\rm{U}}}} {{\varphi _i}} $ | (9) |
式中,S为速度扰动量的功率谱密度,其波数的下边界kL为2 cpm(每分钟波的数量, count per minute),上边界kU为10 cpm.
迭代计算过程中,设定最大波数(kmax)为200 cpm,波数步长为2 cpm.迭代停止的条件有二:其一,相近两次计算的Kolmogorov波数(kc)之差的绝对值不大于2 cpm;其二,kc大于kmax.并基于公式(10)、(11)估算ε[13].
迭代计算确定波数的上下限(L,U),并计算区间[L,U]的S2,进而依据下式计算ε:
| $ \varepsilon = 7.5v\overline {{{\left( {{\partial _{\rm{z}}}\overrightarrow {{u^\prime }} } \right)}^2}} $ | (10) |
式中,υ为动力粘性系数,由此可通过公式(11)计算kc, 即:
| $ k_{\rm c}=\left(\frac{\varepsilon}{v}\right)^{1 / 4} $ | (11) |
水-气之间的热量交换驱动水柱中水温的垂向分布,进而通过水体分层、混合影响湍流演变.水-气之间的热量交换主要包括感热、潜热、长波辐射及短波辐射.其中短波辐射为太阳辐射向下传输,因而气象观测站所获取的短波辐射基本可近似于水面上的短波辐射;利用风场、气压、气温、短波辐射、相对湿度、云量及表层水温等计算水体的感热、潜热、长波辐射,由此结合太阳短波辐射计算水体获得的净热量通量(Rn)[27-30].计算过程简述如下:
水体获取的短波辐射通量(Qs):
| $ Q_{\mathrm{s}}=Q_{\mathrm{s0}}(1-\alpha) $ | (12) |
式中,Qs0为下行短波辐射通量, α为短波辐射的水面反照率.
水体获取的长波辐射通量(HLW):
| $ H_{\mathrm{LW}}=\gamma \cdot \sigma \cdot T_{\mathrm{w}}^{4}\left(0.05 e_{\mathrm{a}}-0.39\right) B_{\mathrm{c}}-4 \gamma \cdot \sigma \cdot T_{\mathrm{w}}^{3}\left(T_{\mathrm{w}}-T_{\mathrm{a}}\right) $ | (13) |
式中,γ为水的长波发射率;σ为斯蒂芬波尔兹曼常数;Ta和Tw分别为气温和表层水体的温度;ea为大气中的水气压;Bc为云量订正因子(Bc=(1-0.72C),C为云量(成数)).
水体获取的感热通量(Hsen):
| $ H_{\mathrm{sen}}=\rho_{\mathrm{a}} \cdot \xi_{\mathrm{a}} \cdot U \cdot \kappa_{\mathrm{s}}\left(T_{\mathrm{w}}-T_{\mathrm{a}}\right) $ | (14) |
式中,ρa为大气密度, ξa为大气比热容, κs为感热转换系数, U为风速.
水体获取的潜热通量(HLat):
| $ H_{\mathrm{Lat}}=\rho_{\mathrm{a}} \cdot L_{\mathrm{e}} \cdot U \cdot \kappa_{1}\left(q_{\mathrm{a}}-q_{\mathrm{sat}}\right) $ | (15) |
式中,qa为大气的比湿,qsat为饱和比湿,κl为潜热转换系数.
水体的净热量通量(Rn)为:
| $ R_{\mathrm{n}}=Q_{\mathrm{s}}+H_{\mathrm{LW}}+H_{\mathrm{sen}}+H_{\mathrm{Lat}} $ | (16) |
鉴于非常规气象站的观测要素通常难以满足热量通量计算的要求(如云量的观测等),因而选取满足计算要求且几何距离相对较近的东山气象站获取的数据.
1.2.4 Monin-Obukhov长度计算在相对稳定状态条件下,风场驱动作用下的水柱表层中水平流速(
| $ \varepsilon(z)=\frac{u_{*}}{\kappa \cdot z} $ | (17) |
式中,κ为卡曼常数.表层浮力通量(Bo)的计算主要依据湖泊水体获取的净热量通量.
| $ B_{\mathrm{o}}=\frac{\alpha \cdot g \cdot R_{\mathrm{n}}}{\rho \cdot C_{\mathrm{p}}} $ | (18) |
式中,α为水的热膨胀系数,ρ为水体密度,Cp为水的比热.则Monin-Obukhov长度(L)[18]:
| $ L=-\frac{u_{*}^{3}}{\kappa \cdot B_{\mathrm{o}}} $ | (19) |
式中,L表征了流场切变与浮力作用湍流产生率的比值,刻画了两种作用对湍流动能产生的贡献比较.
2 结果 2.1 气象场特征鉴于太湖的换水周期长(300天左右),驱动水体分层与混合变化的机械动力主要来源于风场,因而我们给出了观测时段内的风速、风向特征(图 2).从风速变化的整体趋势而言(图 2a),风速呈现递减的趋势;从10月29日至11月2日,每天均存在一个风速峰值,但该峰值也随时间递减. 10月29日和10月30日,其风速最大值为5.7 m/s,后3天,其峰值从3 m/s逐渐递减到2 m/s.从对应的风向分布特征可见(图 2b),4天内,其风向频率最高的是东风,占比为28 %,其对应风速最大为3.5~4 m/s;其次是东南或西北风,各占比基本均小于10 %,总占比在40 % ~50 %之间;其中东南风风速最大达到5 m/s左右.

|
图 2 观测期间东山气象站风速的时序变化(a)以及风向玫瑰图(b) Fig.2 Temporal variation of wind speed (a) and wind direction rose (b) at Dongshan Meteorological Station during observation period |
驱动水体分层与混合演化的另一个作用来源于热力效应,水-气之间的热量交换主要包括水体接受的短波辐射、水-气之间的长波通量的交换、感热及潜热交换(图 3).感热、潜热对水体获取或损失的净热量通量影响甚微(图 3),进而也可说明不同气象站观测的风速差异导致的感热、潜热计算误差占Rn的比重小;水体获取的净热量通量来源于太阳短波辐射,水-气之间的长波交换主要表现为水体能量的损失;从10月30日-11月2日,无论是太阳短波辐射还是净热量通量不仅呈现显著地日变化,而且略呈递减的趋势;晚间水柱主要通过长波辐射的交换造成能量损失,且呈现弱的昼夜变化.

|
图 3 观测期间水-气热力交换通量的时序变化 Fig.3 Temporal changes of heat flux between water and air during observation period |
水柱的温度廓线不仅可以表征温度随时间的变化,同时还能刻画水柱的热力结构,是水体动力、热力作用的综合体现.由图 4可见,水温基本呈现白天升高、晚上递减的周期性变化;10月29、30及31日水温基本不随深度变化,即水温上下基本一致,完全混合;11月1日和2日上下温差超过1℃,存在明显的日分层现象. 11月2日较11月1日的分层现象更明显且持续时间也相对较长.

|
图 4 观测期间水温廓线的时序变化 Fig.4 Temporal variation of water temperature profiles during observation period |
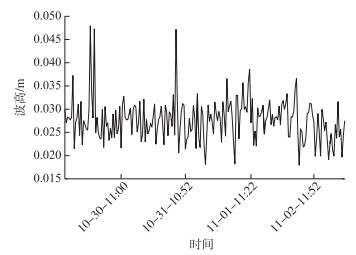
鉴于水体湍流产生与波浪关系密切(波流相互作用形成的朗缪尔环流、波浪破碎等),因而本文给出了观测时段最大波高的时间序列(图 5). 10月29、30及31日均存在较大的波高,使得这3天水体得以混合,上下温差消失. 11月1日、2日波浪呈减弱的趋势,尤其是11月2日减弱显著.另,鉴于观测位置并不位于太湖的开阔处,导致在观测时段中波高和风速的对应关系并不一致,说明风场、热力及波浪的耦合对水体动力影响存在显著的空间分异.
|
图 5 观测期间最大波高的时序变化 Fig.5 Time-varying of maximum wave heights during observation period |
基于ε的物理意义,可知ε可定量描述自然水体中湍流、混合强度及衡量湍流动能演变过程. 图 6a给出了观测时段u、v、w方向上ε时间平均的深度廓线. ε的平均值为10-7.58 m2/s3,最大值出现在表层,最小值出现在2.1 m;在u、v方向上的ε基本接近;w方向的ε最小,其值为10-9.14 m2/s3.在0.7~1.0 m深度区间,ε随深度递减;在1.0~1.9 m的深度区间,其随深度基本呈现稳定状态,即不随深度变化;在1.9~2.1 m区间,ε随深度递减.

|
图 6 观测期间三维ε的廓线分布:(a)时间平均的ε廓线分布;(b)净热量通量对ε的影响;(c)u方向的ε随时间的变化;(d)v方向的ε随时间的变化;(e)w方向的ε随时间的变化 Fig.6 The vertical profiles of the 3D ε during the observation period:(a) Time-averaged ε profiles; (b) Influence of net heat flux on ε profiles; (c)ε change of u with date; (d)ε change of v with date; (e)ε change of w with date |
鉴于热力作用对湍流动能存在产生与抑制的两种作用,因而在观测时段中,以水体获取(损失)净热量通量为依据对观测时段的ε进行平均(图 6b),二者区别很小,仅在w方向的ε廓线中部存在稍明显的差别,即在净热量通量小于零的时段内ε廓线的中部略大.
由于观测时段中含有完整的4天(10月30日、10月31日、11月1日和11月2日),风速逐日减小,净热量通量也呈现出递减的趋势,但递减趋势较缓.因此,分别比较水平方向和垂直方向的ε随日期的变化. 4天内3个方向的ε呈现类同的变化特点:其一,上部随深度递减的特征基本不变;在11月1日和2日出现了ε随水深弱递增的现象,其中11月2日尤甚;其二,中部,呈现随深度稳定不变;在后两天该深度区间的ε有明显升高,且11月2日升高程度最大;后两天随深度维持不变的深度区间较小;其三,底部,后两天的ε随深度递减的趋势逐渐变弱.
3 讨论自然水体中湍流动能主要来源于平均流速切变、波浪动能、浮力效应导致的势能演变等过程,其中仅有浮力过程可能是湍流动能的源或汇[18, 31],另一方面,湍流动能耗散是湍流动能生、消平衡和维持湍流动能变率的关键物理过程,也是评估水体混合机制的关键物理量.
在10月29日至11月2日的观测时段,0.7 m深度以下u、v方向的ε介于10-8~10-7 m2/s3之间;w方向的ε数量级为10-9 m2/s3,接近于ε的背景值[18]. ε的风浪直接作用层、常数层及底边界摩擦混合层的分布特征基本与Callaghan等[18]的结果类似;其中的唯一差别是11月1日、2日在风浪直接作用层与常数层之间的过渡区(图 6c、d、e).
3.1 风浪强迫作用深度上层水体的湍流混合动力主要来源于风场的直接驱动、朗缪尔环流的效应及波浪破碎的作用[18].其中波浪破碎造成波能直接转化为湍流动能,增强表层的ε,但ε随深度衰减剧烈[32],因而直接影响的深度一般在几个波高范围之内[31, 33].鉴于本文采用悬挂式观测,无法观测到该浅表层湍流特征,因而对此不作深入讨论.
在受波浪破碎强烈影响的浅表层以下,主要是由水平流速切变影响的壁层[18, 33],其特征是ε随深度呈反比;ε对深度的依赖弱于浅表层.在本文ε的廓线中(图 6a),各种条件下的ε均存在随深度递减的特征(图 6),其深度基本在1.0 m左右.对应风速为0.2~5.7 m/s(图 2);有效波高基本小于10 cm(图 5).可见,在低中风速条件下,风浪对水柱的直接作用深度为1.0 m左右.
3.2 ε的常数层中热力及朗缪尔环流效应在风浪直接作用深度以下至1.9 m,ε的平均值随深度稳定少变,即为常数层.鉴于风场驱动的流速垂直切变和波浪破碎等湍流产生作用随深度递减,在ε的常数层中,必定存在湍流动能的产生与耗散的平衡,且该湍流动能的产生不仅与深度相对独立,而且其作用深度超过风浪直接作用的深度.从产生湍流动能的物理过程来看,仅有对流作用符合常数层的要求.其中对流产生的机制包含热力和动力两个方面:其一,水体表面热量的损失(感热、潜热和长波)导致的对流;其二,在表层混合层相对较浅的条件下,斯托克斯漂流和风生流的相互作用可能触发朗缪尔环流[32].通常朗缪尔环流存在于表层混合层的底部区间,但在辐合区朗缪尔环流效应产生的对流作用得以向下延伸[18].海洋或深水湖泊中,朗缪尔环流的影响深度远小于其几何深度,因而常数层中的ε主要是热力作用引起的对流效应与之平衡[18];但对浅水湖泊而言,朗缪尔环流效应产生的对流可能伸及底部边界层的顶部.
依据图 3中净热量通量随时间的变化、图 6中太湖在获取(或失去)能量条件下u、v、w方向上ε的时间平均廓线,发现常数层中两种条件下u、v方向的ε基本相同,仅在水体失去能量的条件下w方向的ε略大于水体获得能量的ε.可见在水平方向上,朗缪尔环流的对流输送效应可能占比较大,造成热力效应引起的对流影响基本可以忽略;但在w方向,热力作用引起的对流湍流相对较强,使得在水体失去能量条件下常数层中w方向的ε相对偏大.
总之,太湖中,常数层中的ε可能受到朗缪尔环流及热力效应共同引起的对流作用影响.其中u、v方向上朗缪尔环流作用对常数层的ε作用较大,而w方向上热力效应的影响相对明显.
3.3 动力和热力对ε廓线的影响比较太湖水体深度浅,水体储热能力相对较弱,因而其对气象场的响应迅速,造成水体分层、混合的时间尺度一般为日,甚至更短.水体湍流动能产生来源于机械动力和热力作用.其中机械动力主要包括风浪、朗缪尔环流等过程;热力学效应主要是通过水体获取或损失能量造成的分层、混合之间的转换,进而产生或抑制湍流,另一方面,不同机制产生的湍流所涉及的深度存在差异[34].
鉴于图 6a、6b两图中ε廓线是所有观测时段的平均,因而掩盖了热力和朗缪尔环流对ε影响的差异.本文观测时段包含了4整天,期间风速逐渐减小,净辐射通量的日变化程度相对较弱,因而通过10月30日、31日、11月1日、11月2日的ε廓线分布,可进一步区分风浪和热力作用对ε廓线的影响.
4天u、v、w方向的ε在风浪直接作用层中基本相同;该时段中的后两天上下水温差超过1℃(图 4),除了风浪的直接作用,对流混合对该层中ε的影响在4天平均中并未得到显著体现(图 6a).为此,依据水温的垂向廓线分布特征和ε的位置对温度进行插值,得到在各ε位置上、下5 cm的水温,并计算各ε对应10 cm深度区间的温差时间序列(图 7). 11月1日、2日,风浪直接作用的深度区域,温差远小于下部,且每10 cm区段的温差小于0.1℃(图 7).由此也证实了风浪直接作用层中水体混合程度高、由温差引起的对流很弱,其对ε的影响基本可以忽略.另一方面,鉴于风速逐渐降低,4天中10月30日风速最大,可能是由于观测站点离岸相对较近,东北向的风场对湍流产生的作用可能被弱化,造成4天的风浪作用层深度差别甚微.因为利用ADCP对水体三维流速进行高频观测的要求高,使得此类高频观测持续时间相对较短,从而导致难以定量确定风向对ε的影响.总之,风浪直接作用层中风浪对ε的直接作用突出,温差小且其对ε的影响效应弱.

|
图 7 观测期间每10 cm水柱的温差变化 Fig.7 Difference of water temperature per 10 cm during observation period |
10月30日、31日,水柱基本混合均匀(图 7),u、v、w方向的常数层的起始深度基本维持在1 m左右. 11月1日、2日常数层中的ε不仅大于前两天,更重要的是ε在风浪直接作用层与常数层过渡区有一个明显的向左弯曲,使得常数层起始深度呈现下降的趋势;11月1日、2日存在显著的水体分层;且分层深度一直延伸到1.0~1.2 m(图 6),因而温差明显的区域在1.2 m以下;同时从侧面证实了10月30日、31日朗缪尔环流产生的湍流作用深度可能伸及1.9 m.
在常数层中,与ε平衡的湍流产生不仅来源于朗缪尔环流引发的对流,同时还来源于热力作用.尽管热力作用有促进对流和抑制对流两种作用.就日平均而言,4天内的热力通量相差无几(图 3),但风速减弱却很明显(图 2a),有效波高降低(图 5).另一方面,此4天的L也很弱(图 8),除了10月30、31日少数时段外基本均小于1,随时间推移,波浪、流速切变和朗缪尔环流等动力作用持续减弱,尤其是11月1、2日,L基本接近0,也就是说动力效应远小于热力作用.因而导致朗缪尔环流引发的湍流逐渐减弱,这种次生环流的涡旋直径减小[35],朗缪尔环流造成或输送的湍流作用深度变浅,导致白天热力分层出现(图 7).该区段的水体势能相应增大,正由于晚上水体散失能量导致的对流造成常数层下部ε增大;弱化了底边界层ε随深度递减的程度,同时也说明在11月1日、2日的热力作用对ε的影响明显大于朗缪尔环流引发的湍流.可见在ε的常数层中,朗缪尔环流和热力作用引起的对流是维持ε稳定状态的关键因素,其中朗缪尔环流是影响水体分层的关键过程;朗缪尔环流与热力耦合导致的分层、混合的转换是引起ε增大及其起始高度下移的关键.

|
图 8 观测期间Monin-Obukhov长度的时间序列 Fig.8 Time series of Monin-Obukhov length during observation period |
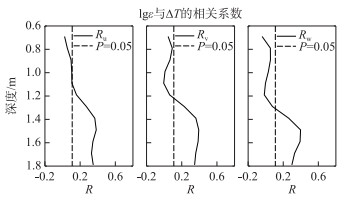
为进一步证实水温的垂直结构对ε的影响差异,利用各层ε和对应深度的温差时间序列的相关性(图 9)分析二者之间的关系. u、v、w方向上分别对应1.1、1.2和1.3 m以上,水温垂直结构与ε无显著关系;上述深度以下,水温的垂向温差与ε存在显著的相关性.鉴于朗缪尔环流对湍流和动量的垂向输送存在显著影响[36],结合图 7的温差分布,可知朗缪尔环流影响水体热量传输和热力分层;由温差导致的湍流对ε的贡献较为突出.
|
图 9 各深度温差与ε的相关系数 Fig.9 Correlation coefficient between temperature difference and ε at each depth |
总之,在中低风速条件下,上表层的风浪直接作用突出,水体混合均匀;朗缪尔环流产生的湍流作用可深及湖泊底边界混合层顶部,同时其强弱也是导致热力分层与混合的关键;热力分层的强度和位置引发的对流混合对常数层和底部边界中的ε贡献显著.
鉴于ADCP观测所需的条件相对较高(如持续供电难以保证),因而观测点选择有电源的中国科学院太湖湖泊生态系统研究站的栈桥头,导致难以定量描述风向对ε的影响;太湖水深较浅,本次观测采用悬挂式,有效观测数据从0.7 m的水深开始,因而波浪破碎和水平速度的垂直切变等各因子对ε的定量影响对湍流动能产生率的贡献难以厘清.
观测时段风场资料是气象局观测的逐时资料,是整点的十分钟平均风场.观测时段的风速小于5.5 m/s.为了考察观测时段的风场是否具有代表性,统计了2017年东山站全年逐时风速资料,发现全年中低于5.5 m/s的风速占全年资料的96.96 %,说明观测时段风场具有较强的代表性;同样辐射通量的日变化也具有典型代表性(图 3).因此尽管观测时段短,但研究结果能较好地反映气象场对大型浅水湖泊中ε的影响效应.
4 结论通过高频野外观测,揭示了太湖ε廓线分布特征,分析动力、热力强迫作用对太湖湍流的作用及深度分布.有利于探讨大型浅水湖泊日分层规律、营养盐和藻类垂向分布及水生生态系统演变. 1)太湖几何深度浅,其ε依然存在典型的3层:随深度递减的ε风浪直接作用层,深度在1.0 m左右以上;基本不随深度变化的常数层,深度区间介于1.0~1.9 m之间;随后是随深度递减的底边界混合层.
2) 太湖中,水平流速切变、波浪等作用导致风浪作用层均匀混合;热力分层的强弱(垂向温差)、位置对常数层和底部边界中的ε贡献显著,甚至造成ε的常数层起始深度下移.
| [1] |
Qin BQ, Zhu GW, Zhang L et al. Wave effects on nutrient release of sediments from Lake Taihu by flume experiments. Science in China: Series D: Earth Sciences, 2005, 35(S2): 33-44. [秦伯强, 朱广伟, 张路等. 大型浅水湖泊沉积物内源营养盐释放模式及其估算方法. 中国科学: D辑:地球科学, 2005, 35(S2): 33-44.] |
| [2] |
Huang L, Fang H, He G et al. Effect of internal loading on phosphorus distribution in the Taihu Lake driven by wind waves and lake currents. Environmental Pollution, 2016, 219: 760-773. DOI:10.1016/j.envpol.2016.07.049 |
| [3] |
Wu T, Timo H, Qin B et al. In-situ erosion of cohesive in a large shallow lake experiencing long-term decline in wind speed. Journal of Hydrology, 2016, 539: 254-264. DOI:10.1016/j.jhydrol.2016.05.021 |
| [4] |
Zheng S, Wang P, Wang C et al. Sediment resuspension under action of wind in Taihu Lake, China. International Journal of Sediment Research, 2015, 30: 48-52. DOI:10.1016/s1001-6279(15)60005-1 |
| [5] |
Wu T, Qin B, Zhu G et al. Modeling of turbidity dynamics caused by wind-induced waves and current in Taihu Lake. International Journal of Sediment Research, 2013, 28: 139-148. DOI:10.1016/S1001-6279(13)60026-8 |
| [6] |
Deng J, Chen F, Liu X et al. Horizontal migration of algal patches associated with cyanobacterial blooms in an eutrophic shallow lake. Ecological Engineer, 2016, 87: 185-193. DOI:10.1016/j.ecoleng.2015.12.017 |
| [7] |
Qin BQ, Hu WP, Chen WM et al. Studies on the hydrodynamic processes and relater factors in Meiliang Bay. J Lake Sci, 2000, 12(4): 327-335. [秦伯强, 胡维平, 陈伟民等. 太湖梅梁湾水动力及其相关过程的研究. 湖泊科学, 2000, 12(4): 327-335. DOI:10.18307/2000.0406] |
| [8] |
Pang Y, Pu PM. Numerical study of wind-driven current in Taihu lake with the air-water coupling model. J Lake Sci, 1996, 8(2): 97-102. [逄勇, 濮培民. 大气-水耦合模式下三维太湖糊流场研究. 湖泊科学, 1996, 8(2): 97-102. DOI:10.18307/1996.0201] |
| [9] |
Hu WP, Pu PM, Qin BQ. A three-dimensional numerical simulation on the dynamics in Taihu lake, China(1): the water level and the current during the 9711 typhoon process. J Lake Sci, 1998, 10(2): 17-25. [胡维平, 濮培民, 秦伯强. 太湖水动力学三维数值试验研究——1.风生流和风涌增减水的三维数值模拟. 湖泊科学, 1998, 10(2): 17-25. DOI:10.18307/1998.0403] |
| [10] |
Xu XF, Liu QQ. Numerical study on the characteristics of wind-induced current in Taihu Lake. Chinese Journal of Hydrodynamics, 2009, 24(4): 512-518. [许旭峰, 刘青泉. 太湖风生流特征的数值模拟研究. 水动力学研究与进展, 2009, 24(4): 512-518.] |
| [11] |
Belcher E, Grant M, Hanley E et al. A global perspective on Langmuir turbulence in the ocean surface boundary layer. Geophysical Research Letters, 2012, 39(18): 9. DOI:10.1029/2012GL052932 |
| [12] |
Brainerd KE, Gregg MC. Diurnal restratification and turbulence in the oceanic surface mixed layer: 1. Observations. Journal of Geophysical Research Oceans, 1993, 98(C12): 22645-22656. DOI:10.1029/93JC02297 |
| [13] |
Baumert HZ, Simpson J, Sündermann J et al. Marine turbulence: theories, observations, and models. Cambridge: Cambridge University Press, 2005: 115-126.
|
| [14] |
Wu H, Patterson GK, Doornm V. Distribution of turbulence energy dissipation rates in a Rushton turbine stirredmixer. Experiments in Fluids, 1989, 8(3/4): 153-160. DOI:10.1007/BF00195789 |
| [15] |
Sreenivasan KR. On the universality of the Kolmogorov constant. Physics of Fluids, 1995, 7(11): 2778-2784. DOI:10.1063/1.868656 |
| [16] |
Doron P, Bertuccioli L, Katz J et al. Turbulence characteristics and dissipation estimates in the coastal ocean bottomboundary layer from PIV data. Journal of Physical Oceanography, 2001, 31(8): 2108-2134. DOI:10.1175/1520-0485(2001)031<2108:TC-ADEI>2.0.CO;2 |
| [17] |
Bluteau CE, Jones NL, Ivey GN. Estimating turbulent kinetic energy dissipation using the inertial subrangemethod in environmental flows. Limnology and Oceanography Methods, 2011, 9(7): 302-321. DOI:10.4319/lom.2011.9.302 |
| [18] |
Callaghan AH, Ward B, Vialard J. Influence of surface forcing on near-surface andmixing layer turbulence in the tropical Indian Ocean. Deep Sea Research Part Ⅰ: Oceanographic Research Papers, 2014, 94: 107-123. DOI:10.1016/j.dsr.2014.08.009 |
| [19] |
Caldwell DR, Lien RC, Moum JN et al. Turbulence decay and restratification in the equatorial ocean surface layer following nighttime convection. Journal of Physical Oceanography, 1997, 27(1997): 1120-1132. DOI:10.1175/1520-0485(1997)0272.0.CO;2 |
| [20] |
Liu ZY, Wei H. Estimation to the turbulent kinetic energy dissipation rate and bottom shear stress in the tidal bottom boundary layer of the Yellow Sea. Progress in Natural Science, 2007, 17(3): 362-369. [刘志宇, 魏皓. 黄海潮流底边界层内湍动能耗散率与底应力的估计. 自然科学进展, 2007, 17(3): 362-369. DOI:10.1080/10020070612331343260] |
| [21] |
Qin BQ, Yang GJ, Ma JR. Dynamics of variability and mechanism of harmful cyanobacteria bloom in Lake Taihu, China. Chinese Science Bulletin, 2016, 61(7): 759-770. [秦伯强, 杨桂军, 马健荣等. 太湖蓝藻水华"暴发"的动态特征及其机制. 科学通报, 2016, 61(7): 759-770. DOI:10.1360/N972015-00400] |
| [22] |
Zhou J, Qin B, Han X et al. Turbulence increases the risk ofmicrocystin exposure in a eutrophic lake (Lake Taihu) during cyanobacterial bloom periods. Harmful Algae, 2016, 55: 213-220. DOI:10.1016/j.hal.2016.03.016 |
| [23] |
Xie P, Xia J, Dou M et al. Research into the effects of the middle route of China's south-to-north water transfer project on water bloom in the middle-down stream of Hanjiang River and the countermeasures Part Ⅰ: An analysis of the key factors generating water bloom in Hanjiang River. Journal of Natural Resources, 2004, 19(4): 418-423. [谢平, 夏军, 窦明等. 南水北调中线工程对汉江中下游水华的影响及对策研究(Ⅰ)——汉江水华发生的关键因子分析. 自然资源学报, 2004, 19(4): 418-423. DOI:10.11849/zrzyxb.2004.04.002] |
| [24] |
Huisman J, Arrayãs M, Ebert U et al. How do sinking phytoplankton speciesmanage to persist?. American Naturalist, 2002, 159(3): 245-254. DOI:10.1086/338511 |
| [25] |
Goring DG, Nikora VI. Despikingacoustic dopplervelocimeter data. Journal of Hydraulic Engineering, 2002, 128(1): 117-126. DOI:10.1061/(ASCE)0733-9429(2002)128:1(117) |
| [26] |
Singh SK, Debnath K. Combined effects of wave and current in free surface turbulent flow. Ocean Engineering, 2016, 127: 170-189. DOI:10.1016/j.oceaneng.2016.10.014 |
| [27] |
Maggiore A, Zavatarelli M, Angelucci MG et al. Surface heat and water fluxes in the Adriatic Sea: seasonal and interannual variability. Physics and Chemistry of the Earth, 1998, 23(5/6): 561-567. DOI:10.1016/s0079-1946(98)00070-6 |
| [28] |
Churchill JH, Kerfoot WC. The impact of surface heat flux and wind on thermal stratification in portage lake, Michigan. Journal of Great Lakes Research, 2007, 33(1): 143-155. DOI:10.3394/0380-1330(2007)33[143:tioshf]2.0.co;2 |
| [29] |
Kim TW, Cho YK. Calculation of heat flux in amacrotidal flat using FVCOM. Journal of Geophysical Research Oceans, 2011, 116(C3). DOI:10.1029/2010JC006568 |
| [30] |
Zhao Q, Sun J, Zhu G. Simulation and exploration of themechanism underlying the spatiotemporal distribution of surfacemixed layer depth in a large shallow lake. Advances in Atmospheric Science, 2012, 29(6): 1360-1373. DOI:10.1007/s00376-012-1262-1 |
| [31] |
Gemmrich JR, Farmer DM. Near-Surface turbulence in the presence of breaking waves. Journal of Physical Oceanography, 2004, 34(5): 1067-1086. DOI:10.1175/1520-0485(2004)034<1067:NTITPO>2.0.CO;2 |
| [32] |
Burchard H, Craig PD, Gemmrich JR et al. Observational and numericalmodelingmethods for quantifying coastal ocean turbulence andmixing. Progress in Oceanography, 2008, 76(4): 399-442. DOI:10.1016/j.pocean.2007.09.005 |
| [33] |
Thorpe SA, Osborn TR, Jackson JFE et al. Measurements of turbulence in the upper-ocean mixing layer using autosub. Journal of Physical Oceanography, 2003, 33(1): 122-145. DOI:10.1175/1520-0485(2003)033<0122:MOTITU>2.0.CO;2 |
| [34] |
Polton JA, Belcher SE. Langmuir turbulence and deeply penetrating jets in an unstratified mixed layer. Journal of Geophysical Research, 2007, 112(C9): C09020. DOI:10.1029/2007jc004205 |
| [35] |
Mazumder BS, Ojha SP. Turbulence statistics of flow due to wave-current interaction. Flow Measurement & Instrumentation, 2007, 18(3/4): 129-138. DOI:10.1016/j.flowmeasinst.2007.05.001 |
| [36] |
Araujo M, Dartus D, Maurel P et al. Langmuir circulations and enhanced turbulence beneath wind-waves. Ocean Modelling, 2001, 3(1/2): 109-126. DOI:10.1016/s1463-5003(01)00004-x |
 2019, Vol. 31
2019, Vol. 31 
