(2: 南京信息工程大学应用气象学院, 南京 210044)
(3: 南京信息工程大学无锡研究院, 无锡 214105)
(4: 耶鲁大学森林与环境研究学院, 纽黑文 CT 06511)
(2: School of Applied Meteorology, Nanjing University of Information Science & Technology, Nanjing 210044, P. R. China)
(3: NUIST-Wuxi Research Institute, Wuxi 214105, P. R. China)
(4: School of Forestry and Environmental Studies, Yale University, New Haven, CT 06511, USA)
湖泊是地球系统的重要组成部分.相对于周围陆地,湖泊的反照率低,比热容大,热导率高,表面粗糙度小,湖泊会储存更多的太阳辐射,产生更高的潜热通量,感热通量则较低[1-4].湖泊与陆地之间存在热力差异,会激发湖-陆环流,进而影响湖岸空气污染物的扩散[5].同时湖泊蒸发也为当地大气提供水汽,对下游降水有增强作用,对局地和区域气候产生影响[5-9].除此之外,湖泊通过蒸发过程参与区域水循环[10-11],特别是对于封闭水体,蒸发会对湖泊水位产生直接影响[12],进而影响湖泊水质[13].因此,寻求合适的方法来研究湖-气交换过程对于评价流域大气环境、预报近地表天气、研究区域水分循环、评估湖泊水质有重要意义[14].
准确量化湖泊水热通量主要有试验观测和数值模拟两种方法.近年来,虽然涡度相关观测(Eddy Covariance, EC)作为一种准确、直接、无干扰的原位通量观测技术被广泛应用[15-19],但由于维护难度大、成本高,获得长期完整的湖-气通量仍然困难.因此随着计算机技术的发展,研究者开发了各种一维、二维、三维湖泊模型[20-23]用于填补观测数据缺失,模拟湖-气通量的长期变化.其中,一维湖泊模型计算量相对较小,运行效率高,且对湖泊水热通量模拟准确,适合与全球区域和气候模式耦合,被广泛应用[12, 20-21, 24-27].其中应用比较广泛的一维湖泊模型是CLM4-LISSS(Community Land Model version 4-Lake, Ice, Snow and Sediment Simulator)模型,它是通用陆面过程模式CLM4的湖泊过程方案,已被应用于不同大小、深度和纬度的湖泊[20, 25-26],并被集成至大气环流模型和数值天气预报模型中[28].而数值天气预报模型预测湖泊天气、气候依赖于湖泊模型提供热量通量、水汽通量和动量通量作为下边界条件,因此对一维模型进行离线调整及多方面评估,对于理解模型计算的物理过程是否合理有重要意义.
不同时间尺度的湖泊水热通量受不同的气象因素和物理过程控制. EC观测结果表明,在半小时到日尺度上,湖泊潜热通量(LE)主要由湖-陆之间的水汽压差和风速协同控制,而感热通量(H)差异则与湖-陆间的温度梯度差和风速密切相关[16, 18].在天气系统尺度上,天气尺度天气系统带来的暖干气流或者冷锋带来的大风天气造成了LE“脉冲”[29-30].在月尺度及以上,辐射能量则是控制水热通量变化的主要原因[31-32].而在气候变化背景下更长时间尺度上,冰期缩短引起地表反照率变化和温度升高导致的波文比变化,改变了能量分配比例,是驱动LE变化的重要因素[33].因此在不同时间尺度上对CLM4-LISSS进行离线评估分析是非常必要的.
过去,研究者们评估了CLM4-LISSS模型在日到年尺度上对不同湖泊的湖-气通量的模拟能力.例如,Subin等[20]将CLM4-LISSS应用于Sparkling湖并评估了模型模拟日平均和10日平均的水热通量的能力. Deng等[34]利用太湖2010年8月17日至26日实测资料将CLM4-LISSS模型本地化后,评估了其在小时到日尺度的表现.之后,Hu等[32]将模型模拟的5日平均表面通量数据与太湖一年的涡度相关观测数据做了比较研究,认为模型能成功模拟太湖的年平均蒸发量. Stepanenko等[35]和Thiery等[36]也分别将模型运用于小型高纬度湖泊和大型深水热带湖泊,在月尺度上评估了模型的适用性.但是,利用多年的原位连续的通量观测资料验证年尺度上CLM4-LISSS适用性的研究未见报道.
太湖是典型的亚热带浅水湖泊,太湖流域也是我国城市化进程最快的区域.因此本文依托太湖中尺度通量网[37],利用太湖避风港站2012-2016年5年辐射及小气候观测资料驱动CLM4-LISSS模型,并利用涡度相关通量数据和湖表面温度数据检验模型模拟结果,验证该模型在半小时、3日、季节、年尺度的适用性,以期提高CLM4-LISSS对太湖年尺度湍流通量的模拟能力.
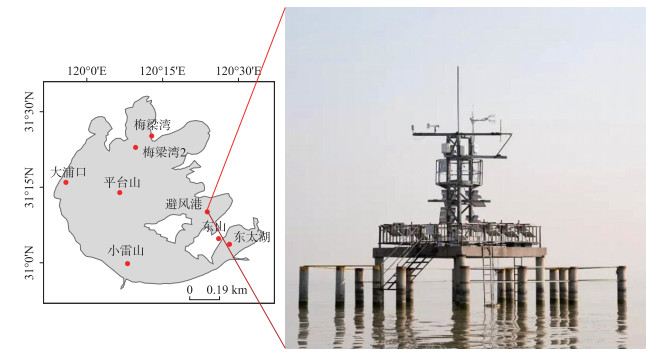
1 材料与方法 1.1 研究区域概况本文以太湖为研究对象.太湖位于长江下游流域,地处江苏省和浙江省交界,平均水深1.94 m,最大水深2.65 m,是典型的亚热带浅水湖泊.基于本项目组前期的研究,太湖上各个通量站月尺度以上的蒸发量相同,即太湖月蒸发量没有空间差异[17],同时说明各个通量站的观测结果都有代表性.因此本文选择了观测时间长,缺失数据最少,且距岸4 km左右,风浪区足够大的避风港站点(BFG:31°10′28″N,120°24′01″E; 图 1).
|
图 1 太湖中尺度通量网避风港站点位置及观测平台 Fig.1 The location of Bifenggang site in Lake Taihu and observation platform |
BFG站点观测始于2011年12月,开展了涡度相关、辐射、气象要素及水温梯度观测. BFG配备有两套CO2/H2O涡度相关系统,架设高度距离水面8.5 m,由三维超声风速仪(型号CSAT3, Campbell Scientific Inc., Logan, UT, USA)和开路式红外气体分析仪(型号EC150, Campbell Scientific Inc., Logan, UT, USA)组成,测量三维风速及大气中水汽和二氧化碳浓度,数据采样频率为10 Hz;动量通量、感热通量(H)和潜热通量(LE)数据输出步长为30 min.辐射数据由四分量辐射计观测获得(型号CNR4, Kipp & Zonen B. V., Delft, the Netherlands),架设高度距离水面3.0 m.小气候系统(型号Dynakmet, Dynamax Inc., Houston, TX, USA)同样架设在距离湖面8.5 m处,用于测量空气温度、大气压强、相对湿度、风速及风向等气象要素.湖深20、50、100、150 cm和底泥的温度使用水温计(型号109-L, Campbell Scientific Inc., Logan, UT, USA)测量.辐射、气象要素、水温梯度数据采样频率为1 min,由数据采集器(型号CR1000,Campbell Scientific Inc., Logan, UT, USA)收集,输出步长为30 min.
1.2 数据处理 1.2.1 数据插补气象、辐射数据与通量数据的空缺采用不同的方法进行插补.空气温度、水汽压、风速、大气压数据的缺失率较低,2012年及2016年无数据缺失,2013-2015年内最大缺失率分别为0.3196 %、0.3368 %、0.3767 %和0.3653 %.辐射数据缺失率在0.0398 % ~20.2527 %之间. 2012-2016年BFG站半小时LE(H)数据的缺失率分别为30 % (29 %)、12 % (11 %)、23 % (22 %)、20 % (16 %)和21 % (19 %).
对于缺失较少(一天内少于5个数据点)的气象数据(风速除外)、辐射数据和通量数据进行线性内插.对于数据空缺较大的气象数据和辐射数据,将BFG站分别与中尺度通量网其他4个站点(大浦口站DPK、梅梁湾站MLW、平台山站PTS和小雷山站XLS)的气象、辐射数据建立线性关系,选择相关性最好的站点,利用2个站点间现有数据的线性关系插补缺失数据.对于空缺较大的通量数据,优先利用BFG本站的另一套EC数据建立线性关系进行插补,剩余的缺失数据,利用插补得到完整的各项气象数据序列,根据物质传输的相关理论插补完整[38-39].
1.2.2 湍流通量的能量闭合校正虽然EC方法可以对湍流通量进行直接观测,但其仍在存在着能量平衡不闭合的问题[40-41].本文采用能量平衡闭合度(Energy Balance Closure, EBC)来定量评价太湖的能量闭合度:
| $ E B C=\frac{L E+H}{R_{\mathrm{n}}-\Delta Q} $ | (1) |
式中, Rn为净辐射,ΔQ为水体热储量.能量平衡不闭合可能导致观测的H、LE偏低[42].通常采用假设波文比(BRER)法来调整感热和潜热通量,即认为波文比的观测值是正确的,将多余的可利用能量按照波文比分配给感热通量和潜热通量:
| $ B R E R=\frac{H}{L E} $ | (2) |
| $ L E_{*}=\frac{R_{\mathrm{n}}-\Delta Q}{1+B R E R} $ | (3) |
| $ H_{*}=R_{\mathrm{n}}-\Delta Q-L E_{*} $ | (4) |
式中, LE*和H*分别为强迫能量闭合后的潜热通量和感热通量.由于波文比法在半小时尺度上将产生不合理的BRER值,因此无法针对半小时的潜热和感热通量数据进行修正.根据本课题组前期研究[43]可知,能量闭合度随着时间尺度延长会有所增大,在更长的时间尺度上做能量平衡闭合校正效果越好,因此对3天、月和年尺度的数据分别进行了各自尺度的能量平衡闭合校正.
1.2.3 湖表温度反算湖表温度为湖体顶层与大气之间无穷小的交界面处的温度.湖表温度(Ts)的观测值是基于斯蒂芬-玻尔兹曼定律根据天空长波辐射和湖表发射长波辐射的观测值反算获得:
| $ T_{\mathrm{s}}=\left(\frac{L_{\uparrow}-(1-\varepsilon) L_{\downarrow}}{\varepsilon \cdot \delta}\right)^{\frac{1}{4}} $ | (5) |
式中, L↑为湖表发射的长波辐射,L↓为天空长波辐射,湖表比辐射率ε=0.97,δ为斯蒂芬-玻尔兹曼常数(5.670040×10-8).
1.3 CLM4-LISSS模型介绍及参数设置CLM4-LISSS模型是由美国国家大气研究中心和劳伦斯伯克利国家实验室研发的,由CLM3.5-Lake改进而来[20].模式中利用大气强迫场,通过湖表薄层能量平衡来求解湖表温度和表面通量.湖表薄层的能量平衡方程如下:
| $ \beta\overrightarrow{ S_{\mathrm{g}}}-\overrightarrow{L_{\mathrm{g}}}-H-L E-G=0 $ | (6) |
式中,β为被保留在湖泊表层的短波辐射的比例;
| $ H=-\rho_{\text {atm }} \cdot C_{\mathrm{p}} \frac{\left(\theta_{\text {atm }}-T_{\mathrm{s}}\right)}{r_{\mathrm{ah}}} $ | (7) |
| $ L E=-\lambda \cdot \rho_{\mathrm{atm}} \frac{\left(q_{\mathrm{atm}}-q_{\mathrm{sat}}^{T_*}\right)}{r_{\mathrm{aw}}} $ | (8) |
| $ G=\frac{2 \lambda_{\mathrm{T}}}{\Delta z_{\mathrm{T}}}\left(T_{\mathrm{s}}-T_{\mathrm{T}}\right) $ | (9) |
式中, ρatm为湿空气密度;Cp为空气比热容;θatm为大气位温;Ts为湖表温度;rah为大气对热量输送的阻力;λ为汽化潜热;qatm为大气比湿;qsatTs为湖表温度Ts下的饱和比湿;raw为大气对水汽输送的阻力;λT为湖泊顶层的热导度;ΔzT和TT分别为湖泊顶层的厚度与温度.
模型参数分为内部参数和外部参数.内部参数一般不需要经常调试,是相对普适性的参数,包括分子扩散系数和湍流扩散系数ke等.在本研究中,分子扩散系数与原模型一致,为常数(1.433×10-7 m2/s).但是原模型中默认的湍流扩散系数并不适用于浅水湖泊,需要调整. Deng等[34]发现如果采用默认的湍流扩散系数,模型无法模拟出夏季太湖湖体温度垂直分层的特征,且湖表温度的日较差也远小于观测值,这表明ke的默认值量级过大,使得模拟的湖水湍流混合作用过强.为了使湖水温度的日变化模拟结果更符合实际情况,Deng等[34]通过对比湖表温度和湖体水温廓线的模拟结果和观测结果,对湍流扩散系数进行了优化,将ke设置为原模型取值的2 %.本研究沿用Deng等的取值.
外部参数依站点情况而定,如短波辐射被保留在湖泊表层的比例(β)和粗糙度常数等,需要针对观测站点进行优化.对于参数β,原模型取值为0.4,依据是净短波辐射中近红外辐射所占的比例.本文参照Deng等[34]将β与消光系数η通过比尔定律联系起来,即:
| $ \beta=1-\mathrm{e}^{-z_{{\rm a}} \eta} $ | (10) |
式中, za为湖体第一层的厚度,模式中设置为0.2 m. η越大,水体越浑浊,则会有更多的辐射能量被截留在湖表薄层.张运林等[44-45]测量了太湖13个站点的消光系数,得出太湖消光系数大约在1.50~4.59 m-1之间,这为本研究的参数优化提供了边界条件.本研究通过多组敏感性分析,以年尺度上潜热通量模拟效果最优为目标,得到η的最适值为2.5 m-1,即β等于0.393.
对于粗糙度长度,原模式中粗糙度长度参数化方案根据Smith[46]在海上强风情况(6 m/s)的观测结果取值.但BFG站的风速较弱,2012-2016年的平均风速仅为4.3 m/s,因此采用原参数化方案不适用于太湖. Deng等[34]根据2010年8月17日至26日梅梁湾站(MLW)的观测值修改了参数化方案,将粗糙度长度设置为常数,明显改善了模型对湖表温度以及潜热通量日变化过小的问题.本研究针对粗糙度长度取值测试了两种优化方案:(1)参照Deng等[34]的设置,将粗糙度设置为常数,基于年平均潜热通量模拟值和观测值的对比结果,优化了粗糙度长度,但是在模拟过程中,半小时的潜热通量模拟结果出现了多个大于600 W/m2的异常值,这些异常值通常发生在风速≥6.32 m/s的条件下;(2)基于BFG站实际观测数据反算的粗糙度长度[47],将粗糙度长度在弱风和强风条件下分段表达.根据Xiao等[47]的研究结果,将粗糙度长度表达为:
当风速<7 m/s时,
| $ z_{0 \mathrm{m}}=3.3 \times 10^{-4} \mathrm{m} $ | (11) |
| $ z_{0 {\rm h}}=1.9 \times 10^{-7} \mathrm{m} $ | (12) |
| $ z_{0 \mathrm{q}}=7 \times 10^{-6} \mathrm{m} $ | (13) |
当风速≥7 m/s时,
| $ z_{0 \mathrm{m}}=3.3 \times 10^{-4} \mathrm{m} $ | (14) |
| $ z_{0 {\rm h}}=1.07 \times 10^{-3} \mathrm{m} $ | (15) |
| $ z_{0 \mathrm{q}}=8.9 \times 10^{-7} \mathrm{m} $ | (16) |
式中,z0m、z0h、z0q分别为动量粗糙度长度、热量粗糙度长度和水汽粗糙度长度.
1.4 评价指标本研究利用各时间尺度上EC观测的水热通量作为参考来评价模型表现,所用的评价指标包括决定系数(R2)、一致性指数(IOA)和平均偏差(ME)、均方根误差(RMSE).
IOA计算公式为:
| $ IOA = 1- \frac{{\sum\limits_t {{{\left( {{o_i}- {p_i}} \right)}^2}} }}{{\sum\limits_i {{{\left( {\left| {{p_i}- \overline {{o_l}} } \right| + \left| {{o_i}- \overline {{o_l}} } \right|} \right)}^2}} }} $ | (17) |
式中,pi和oi分别为模拟值与观测值; ol为观测的平均值. IOA=1时表示模拟值与实测值完全一致,IOA=0时表示二者完全不同.
ME表示模拟值与观测值之间的平均偏差大小,ME>0,代表模拟存在高估;ME < 0,代表模拟存在低估. ME计算公式为:
| $ ME = \frac{1}{N}\sum\limits_{i = 1}^N {\left( {{p_i}- {o_i}} \right)} $ | (18) |
RMSE是模拟值与真值偏差的平方和观测次数比值的平方根,对特大或特小误差反应比ME更加敏感.计算公式如下:
| $ RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{p_i}- {o_i}} \right)}^2}} } $ | (19) |
由公式(7)和公式(8)可知,能否精确地模拟湖表温度Ts对于评估模型的表现至关重要. CLM4-LISSS模型中H的计算需要湖表温度和参考高度大气温度差(Ts-Ta),而LE除与风速、大气稳定度有关外,也与湖表的水汽压和参考高度的水汽压之差相关,湖表的水汽压等于Ts下的饱和水汽压.因此,我们先验证模型模拟Ts的能力.
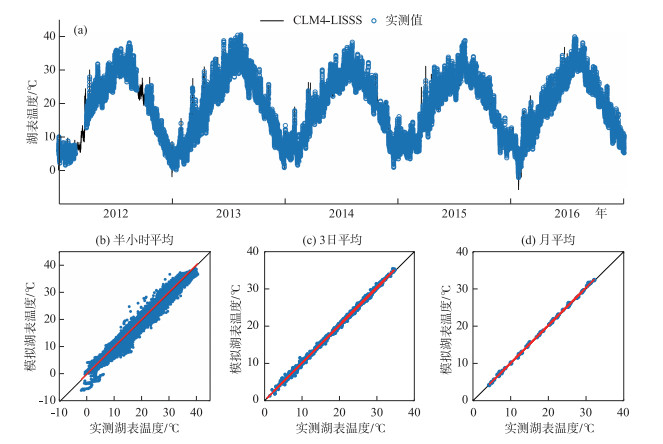
模型能很好地模拟出半小时尺度上Ts的变化趋势(图 2a).模拟与观测的Ts均在冬季最低,夏季最高,能很好地模拟Ts的季节趋势.模型模拟值与观测值的散点图接近1:1线,R2达到了0.986,但截距为0.19±0.01℃,模拟存在整体偏高的情况(图 2b). ME和RMSE分别为0.24和1.06℃.总的来说,CLM4-LISSS模型在半小时尺度上能模拟出Ts的逐时变化趋势.
|
图 2 2012-2016年湖表温度的模拟值与观测值对比图(半小时尺度时间序列图(a);半小时尺度1 :1图(b);3日尺度1 :1图(c);月尺度1 :1图(d)) Fig.2 Comparison of simulated and observed lake surface temperature from 2012 to 2016(time series at half-hourly scale(a); 1 :1 plot at half-hourly scale(b); 1 :1 plot at 3-day scale (c); 1 :1 plot at monthly scale (d)) |
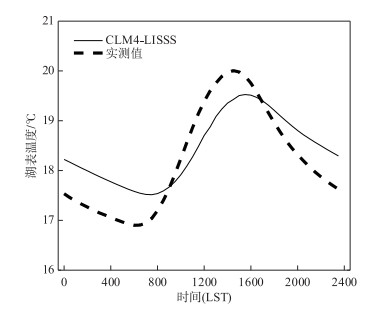
Ts模拟值的日组分与观测值相比存在时间滞后(图 3).观测的Ts于当地时间06:30达到最低值16.9℃,而模拟值于08:00达到最低值17.5℃.达到最高值的时间也有所滞后,模拟值于16:00达到最大值19.52℃,而观测值则提前1小时,于15:00达到最大值.模拟值的日较差(2.0℃)相比于观测值(3.1℃)较小.模拟所得湖表温度白天小于观测值,而夜间大于观测值.这一现象也出现在了Deng等[34]的模拟中.这是因为本研究为保证年均潜热通量模拟准确,模型中消光系数设置略小,而较小的消光系数,导致模型白天未能截留足够的太阳辐射于湖表,能量向下传输,湖体增温相较观测略大;而在夜晚,湖表快速降温,而湖体温度下降缓慢,湖表与湖体之间的温度差,形成了不稳定的温度层结,触发了模式的对流混合机制,而白天模式中储存在湖体中的能量大于实际储存在湖体中的能量,模拟的湖体温度高于实际湖体温度,导致模型模拟夜晚湖表温度偏高.
|
图 3 湖表温度的观测值和模拟值的日组分图 Fig.3 Diurnal composite of simulated and observed lake surface temperature |
模型在3日尺度、月尺度上Ts模拟结果与观测结果非常吻合.线性回归曲线接近1 :1线(斜率接近1,且截距小于0.04℃),相关系数和一致性系数也接近1(图 2c,图 2d). 表 1也显示3日尺度和月尺度上的RMSE分别为0.55、0.34℃,明显低于半小时尺度的统计参数.这表明模式能很好地模拟出Ts的逐日变化和季节变化.
| 表 1 不同时间尺度的湖表温度、潜热通量和感热通量模拟统计参数 Tab. 1 Statistical parameters of Ts, LE and H at different time scales |
在年尺度上,2012-2016年的年均Ts模拟值分别为17.81、18.67、18.27、18.38和18.96℃,而观测值分别为17.77、18.39、18.11、18.22和18.60℃,模型对年平均Ts只有0.24℃的高估,RMSE只有0.18℃,模型对年平均Ts模拟效果非常理想.
2.2 能量通量评估结果 2.2.1 潜热通量在半小时尺度上,LE的观测值和模拟值对比如图 4a和4b所示.模式能模拟出半小时LE的逐日变化和季节变化趋势,模拟值与观测值建立的线性回归线斜率等于1.1±0.004;但是却存在明显高估的情况,即截距相对较大(17.4 W/m2).半小时尺度的ME和RMSE分别为22.1和39.4 W/m2(表 1).

|
图 4 2012-2016年潜热通量的模拟值与观测值对比图(半小时尺度时间序列图(a);半小时尺度1 :1图(b);3日尺度1 :1图(c);月尺度1 :1图(d)) Fig.4 Comparison of simulated and observed latent heat flux from 2012 to 2016(time seires at half-hourly scale (a); 1 :1 plot at half-hourly scale(b); 1 :1 plot at 3-day scale (c); 1 :1 plot at monthly scale (d)) |
在半小时尺度上,LE模拟存在偏差主要有两个方面的原因.首先,在模型系统里,能量平衡是闭合的,但是涡度通量观测值在半小时尺度上未强迫能量平衡闭合(强迫闭合结果超出合理范围),即H与LE之和小于可利用能量,2012-2016年通量数据的总体能量平衡闭合度为0.68.其次,模拟值和观测值对比结果的离散程度较高(图 4b),除了上述原因以外,还可能与消光系数的影响有关.在实际情况下,由于太湖是大型浅水湖泊,对大气响应迅速,风场变化会影响消光系数.但是模型中将消光系数设置为常数,这会引起模拟结果的偏差.
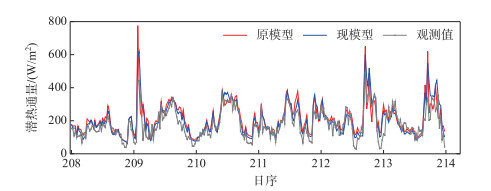
与原模型中采用海表粗糙度方案模拟的LE相比,现粗糙度方案明显改善了模型对于LE极值模拟偏大的问题.使用原模型的默认粗糙度方案,LE模拟值会出现异常高值,2013年7月29日、31日、8月1日模拟出了大于600 W/m2的异常高值(775.55、650.30、619.94 W/m2),分别对应z0q为1.56×10-4、4.08×10-6、2.29×10-5 m,显著高于根据BFG涡度相关数据反算的z0q(8.9×10-7 m),过大的z0q导致了模型在高风速条件下失灵. 图 5展示了2013年7月28日至8月2日模型模拟结果,其中观测值为插补过后的半小时潜热通量.无论是否修改粗糙度长度,模型都能很好地模拟出LE变化趋势,但修改粗糙度长度方案后模型的异常高值明显下降,更接近观测的LE.改进后的模型除对异常高值有改进外,半小时尺度上的统计参数也有所提高,一致性系数IOA增加了0.02, ME和RMSE减小约2 W/m2,R2由0.69提高至0.73.但虽然修改了粗糙度长度方案,模型对于高风速状态下的LE仍然存在高估.从图 4a可知,模型模拟的LE出现了9个大于500.0 W/m2的异常点.但是,由于天气原因或仪器故障,其中6个对应的观测数据缺失.剩余的3个异常点LE模拟值分别为562.0、534.4和501.5 W/m2,对应观测值分别为191.7、250.4和109.3 W/m2,分别对应风速9.94、8.55和7.32 m/s.其它6个模拟异常值出现时,风速处于9.97~11.85 m/s,且通过插补得到的观测值虽然大于400.0 W/m2,但小于500.0 W/m2.由此可知,现有模型对半小时尺度上强风状态下LE的模拟仍有待改进.
|
图 5 2013年7月28日至8月2日逐日潜热通量观测与模型对比图 Fig.5 Comparison of simulated and observed latent heat flux at half-hourly scale from July 28 to August 2 in 2013 |
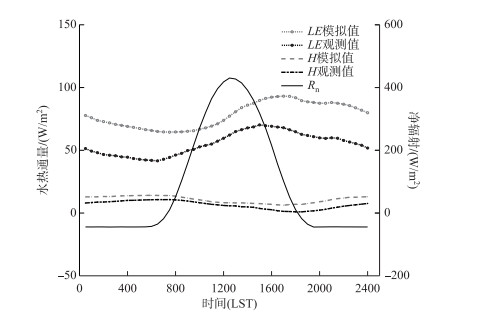
模拟的LE的日组分也存在时间滞后的问题(图 6).模拟的LE在7:30之前达到最小值(64.5 W/m2),相比于观测值(41.6 W/m2)滞后1小时.模拟值于17:00达到最大(93.1 W/m2),相比于观测值(70.3 W/m2)滞后2小时. LE模拟值的时间滞后与Ts模拟值滞后的相位一致(图 3).但是白天模拟的湖表温度低于观测,模拟的LE却大于观测值,这主要是因为观测的湍流通量存在能量不平衡的现象,在半小时尺度上2012-2016年间观测的总体能量平衡闭合度只有0.68.如果仅将能量平衡闭合度在0.9~1.1范围的数据用于对比,ME(14.2 W/m2)和RMSE(37.8 W/m2)有所下降,R2(0.82)与IOA(0.94)有所上升.
|
图 6 净辐射观测值与感热通量、潜热通量观测值和模拟值的日组分 Fig.6 Diurnal composite of observed net radiation and simulated and observed sensible and latent heat flux |
与半小时尺度上模拟的潜热通量与观测值的对比相比(图 4b),在3日平均尺度上模拟值与经能量闭合校正后的观测值对比(图 4c)效果更好. 图 4c中,数据点紧密分布在1 :1线附近(斜率=0.87±0.02,截距=9.49 ±1.45 W/m2).观测值与模拟值的变化范围也是相一致的.统计结果也表明,模型在3日尺度上模拟结果较好(R2=0.93,IOA=0.98,RMSE =15.0 W/m2,ME=-1.2 W/m2).
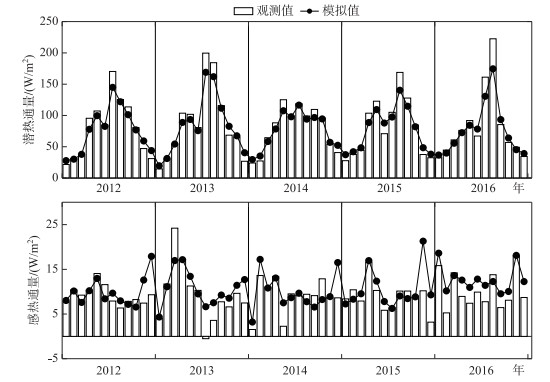
图 7展示了2012-2016年模拟与观测的LE的季节变化(观测数据经过了月尺度能量平衡闭合校正).春季,模拟和观测LE均迅速增加,6月因“梅雨”而减少,7、8月达到最大值.之后随着时间的推移,LE逐渐减小,在冬季达到最小值.模型在高通量月份存在低估现象,在低通量月份偏高(图 4d):从4-8月,模型低估LE约4 %,ME和RMSE分别为-12.0和18.1 W/m2;在剩余时间内,模拟略微高估了LE(ME=2.4 W/m2).造成这些季节性偏差的原因可能有两个.
|
图 7 2012-2016年月平均潜热通量与感热通量观测值和模拟值对比 Fig.7 Comparison of monthly mean latent and sensible heat flux from 2012 to 2016 |
一是模型中底泥热通量计算季节性偏差. Stepanenko等[25]的研究表明关闭模型中底泥温度计算模块,会出现湖表温度和能量通量产生被高估的情况,并且这种偏差存在季节差异.因此,利用Wang等[48]建立的底泥温度与底泥热通量的关系, 分别利用观测和模拟的底泥温度计算了底泥热通量(Gs),结果表明,模型模拟的月平均Gs值在春、夏季节小于观测值,在秋、冬季节大于观测值,但与水体热通量相比,其量级很小(-0.25~0.24 W/m2)可以忽略不计.因此在太湖底泥热通量方案不是潜热通量模拟出现季节性偏差的主要原因.
二是模式中消光系数η被设置为常数,无季节性变化.消光系数决定了湖表层截留的太阳辐射能量的多少.在本研究中,η被设置为一个常数,为2.5 m-1. Zhang等[44-45]的观测结果表明,对于东太湖,由于沉水植被的死亡和分解,冬季的消光系数会增加. Wang等[49]从MODIS-Aqua图像中也推断出,太湖在冬季和春季的浑浊度要高于夏季和秋季.为了确定季节误差是否由消光的季节变化引起,我们将消光系数进行了敏感性测试.结果表明,当η增大到6 m-1时,春季和冬季的LE模拟效果(春季:ME=-2.7 W/m2,R2=0.81;冬季:ME=6.3 W/m2,R2=0.73)将被明显改善.因此,我们将模型的季节差异部分归因于忽略了消光系数的季节性变化.
模拟的2012-2016年年平均LE分别为75.6、83.5、76.8、78.1、76.4 W/m2,实测的年平均LE分别为79.0、87.6、79.2、80.6、82.3 W/m2,CLM4-LISSS模型能很好地模拟出潜热通量的年际变化趋势(R2=0.85,IOA=0.7),但模型对于年均LE模拟略低,ME为-3.7 W/m2(表 1).这证明了CLM4-LISSS模型有模拟年尺度上湖泊蒸发的能力,可以用于长期蒸发变化的模拟.
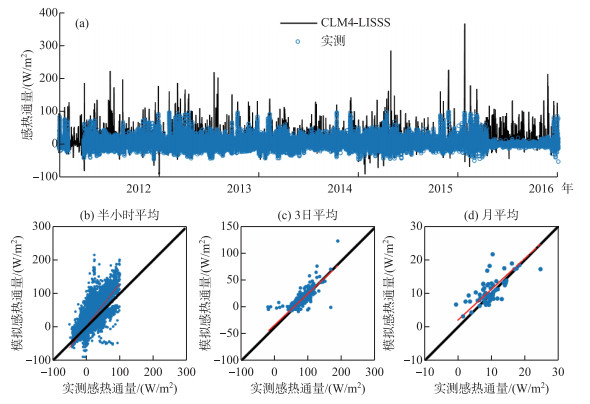
2.2.2 感热通量CLM4-LISSS模拟的半小时H与实测半小时H的一致性不如LE或Ts的一致性强(ME=3.9 W/m2,RMSE =12.4 W/m2,R2=0.57).拟合线的斜率为1.28,模型对H的模拟存在高估.此外,模型对H的模拟还存在很多异常高值(H > 100 W/m2)(图 8a和图 8b),与模拟的LE相似,这主要是由于在半小时尺度上EC观测存在能量不闭合造成的.
|
图 8 2012-2016年感热通量的模拟值与观测值对比图(半小时尺度时间序列图(a);半小时尺度1 :1图(b);3日尺度1 :1图(c);月尺度1 :1图(d)) Fig.8 Comparison of simulated and observed sensible flux from 2012 to 2016 (time series at half-hourly scale(a); 1 :1 plot at half-hourly scale(b); 1 :1 plot at 3-day scale(c); 1 :1 plot at monthly scale(d)) |
感热通量模拟值的日变化与观测趋势相似,但仍存在相位偏差(图 6). H模拟值于17:00达到最小(6.3 W/m2),比H观测值提前了1.5 h.模拟的最大值(14.1 W/m2)出现于06:00,比观测的最大值提前了1.5 h.
经过3日平均尺度上的能量平衡闭合校正后,CLM4-LISSS模拟的H与实测值H有良好的一致性(回归直线斜率为0.94,ME为1.83 W/m2)(图 8c).尽管在能量平衡闭合校正后,模拟的表现有所提高,但是仍然在2013年3月左右出现了3个异常值(模型模拟的H分别为0.6、-3.9、0.91 W/m2,观测值分别为-49.4、-48.3和-44.4 W/m2).经计算发现,在2013年2月26日至3月1日,3月7日至10日和3月19日至22日期间,平均温度梯度差(Ts-Ta)分别为-0.20、-0.73、-0.31℃.在这3个时期,空气温度分别在3天内下降了10.74、14.52、10.52℃,明显大于湖表温度下降的幅度(5.06、7.18、5.82℃).这表明该模型难以准确模拟气温骤降时的H.
H的模拟值与观测值的季节趋势相似,但模拟值与观测值的存在差异(图 7). 2013年3月H模拟的不准确,也导致2013年模拟的年均值偏高. 2013年7月模拟H也与观测到的负值不一致.模拟和实测月平均H之间的ME、RMSE、R2和IOA分别为1.3 W/m2、3.4 W/m2、0.45和0.79.由此可见,在季节尺度上CLM4-LISSS模型可以很好地模拟出H的变化,但对于H值的模拟还有待进一步的提高.
在年尺度上,模型模拟值H与实测值H存在较好的相关性,但未通过显著性检验,两者相差较大(ME=1.3 W/m2,RMSE=0.9 W/m2). 2012-2016年模拟的H值分别为9.9、10.7、9.8、10.4、12.7 W/m2,经年尺度上能量平衡闭合校正后的观测值分别为9.2、9.4、9.0、9.0、10.4 W/m2,模型模拟存在高估H情况.由此可知,在年尺度上CLM4-LISSS模型能出H的变化,但存在一定的高估.
2.3 冷锋过境期间CLM4-LISSS模型的表现上述结果描述了CLM4-LISSS模型在各时间尺度状态下的表现,但没有揭示有天气系统过境时模型的模拟效果.冷锋过境时在几小时到几天的时间尺度上会对湖泊与大气间的湍流热交换产生强烈影响[29-30]. H和LE“脉冲”经常出现在这些冷锋过境事件中,通常伴随着风速的增加、风向的变化以及湿度和空气温度的降低.由于水体比热容大,相对于快速变化的大气温度,湖泊温度变化滞后.这些因素对模型模拟能力提出了严峻考验,因此我们选取了两个冷锋过境时刻(晚秋及冬末)来评估CLM4-LISSS模型表现.
图 9展示了2014年11月29日至12月5日(DOY 333-339)模型的模拟结果.在这一时期,气温从15.2℃迅速下降到6.8℃,风速从0.2 m/s骤增至9.7 m/s.模拟和实测的湖表层温度均随时间呈下降趋势,但模型响应滞后,偏差较大.对于感热通量H,模型总体能够再现观测趋势,但是在12月3日22:00-4日09:00期间,H模拟值从约61.6 W/m2突然增加到138.9 W/m2,而观测值随时间变化却较为稳定.这与热量粗糙度长度参数化方案有关.由于风速超过7 m/s,热量粗糙度长度突然由低值变为高值,导致模拟H迅速上升.相比之下,潜热通量的计算结果较好,模型模拟的LE趋势与整个过程中观测到的LE趋势非常吻合.

|
图 9 2014年11月29日至12月5日(DOY333-339)湖表温度、潜热通量、感热通量模拟与观测对比 Fig.9 Comparison of simulated and observed lake surface temperature, latent and sensible heat flux from 29 September to 5 December (DOY333-339) in 2014 |
在2016年2月11日至17日(DOY 42-48)期间,模型捕捉到了观测到的Ts、LE和H的变化趋势.但在2月12日,风速由1.8 m/s骤增至11.5 m/s, 模型模拟出了风速骤增时H增加的趋势,但高估了H的峰值.水热通量的模拟误差与Ts的误差有关,例如2月12日至14日模拟的Ts偏高,导致H被高估(图 10).
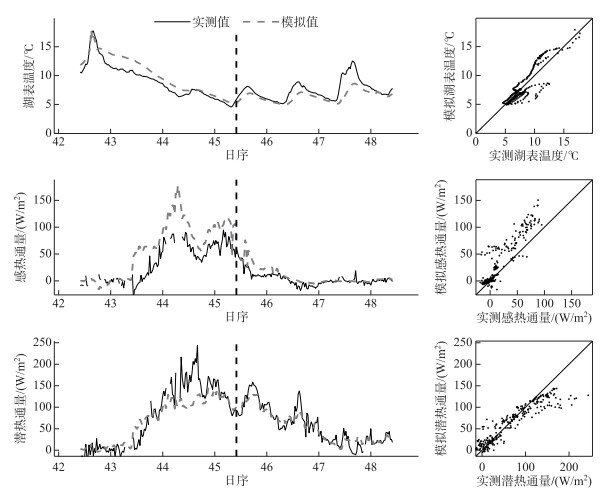
|
图 10 2016年2月11日至2月17日(DOY 42-48)湖表温度、潜热通量、感热通量模拟与观测对比 Fig.10 Comparison of simulated and observed lake surface temperature, and sensible heat flux from 11 to 17, February (DOY42-48) in 2016 |
总的来说,在冷锋过境期间,模型能模拟出水热通量的逐时变化,但在风速较大的情况下,H被明显高估.
3 结论基于2012-2016年太湖小气候数据和辐射数据,驱动CLM4-LISSS模拟了太湖的LE和H,并在不同时间尺度上与EC的观测结果(通量数据在不同尺度上进行了能量平衡闭合校正)进行对比.主要研究结果如下:
1) 在半小时至年尺度上,湖表温度Ts的模拟值与观测结果吻合较好,模型能很好地模拟Ts的逐时变化及季节趋势.不同时间尺度上模拟值与观测值的R2均大于0.97.但是由于模型中消光系数设置略小,导致模拟Ts的日较差小于观测.
2) CLM4-LISSS模拟的潜热通量与EC的观测结果基本一致.调整粗糙度长度方案后的模型有效降低了高风速条件下的LE模拟的异常高值.该模型能较好地再现潜热通量的日变化、季节变化和年变化.模型在春夏两季低估LE值,而在秋冬两季高估LE.这种季节性偏差可能是由于不同季节消光系数设置不变造成的. CLM4-LISSS有模拟年平均湖泊蒸发的能力,可以用于长时间尺度蒸发趋势的研究.
3) 虽然感热通量的日变化、季节变化与EC观测结果的趋势一致,但模拟效果较差.在半小时尺度下,该模型模拟出比观测值更高的峰值,部分原因是观测值的能量平衡不闭合和热量粗糙度长度设置.在月尺度以上的时间尺度上,模拟的H与观测结果相比出现较大偏差.但是模型仍能模拟出年平均H的变化趋势.
4) 本文分别选取了晚秋与冬末两个时间点对冷锋过境期间的模型性能进行了评估. CLM4-LISSS可以模拟出可以冷锋过境期间LE与H的变化趋势,也可以很好地再现冷锋过境期间的LE,但在风速较大的情况下,H被明显高估.
| [1] |
Bonan GB. Sensitivity of a gcm simulation to inclusion of inland water surfaces. Water Resour Res, 1995, 8(11): 2691-2704. |
| [2] |
Eaton AK, Rouse WR, Lafleur PM et al. Surface energy balance of the western and central Canadian subarctic:Variations in the energy balance among five major terrain types. J Clim, 2001, 14(17): 3692-3703. DOI:10.1175/1520-0442(2001)014<3692:SEBOTW>2.0.CO;2 |
| [3] |
Beyrich F, Leps JP, Mauder M et al. Area-averaged surface fluxes over the litfass region based on eddy-covariance measurements. Bound-Layer Meteor, 2006, 121(1): 33-65. DOI:10.1007/s10546-006-9052-x |
| [4] |
Rouse WR, Blanken PD, Bussières N et al. An investigation of the thermal and energy balance regimes of great slave and great bear lakes. Journal of Hydrometeorology, 2008, 9(6): 1318-1333. DOI:10.1175/2008JHM977.1 |
| [5] |
Sills DM, Brook JR, Levy I et al. Lake breezes in the southern Great Lakes region and their influence during BAQS-Met 2007. Atmos Chem Phys, 2011, 11(15): 7955-7973. DOI:10.5194/acp-11-7955-2011 |
| [6] |
Eichenlaub V. Lake effect snowfall to the lee of the Great Lakes:Its Role in Michigan. Bull Amer Meteorol Soc, 1970, 51(5): 403-412. DOI:10.1175/1520-0477(1970)051<0403:LESTTL>2.0.CO;2 |
| [7] |
Samuelsson P, Kourzeneva E, Mironov D. The impact of lakes on the European climate as simulated by a regional climate model. Boreal Environ Res, 2010, 15: 113-129. |
| [8] |
Dai Y, Wang L, Yao T et al. Observed and simulated lake effect precipitation over the Tibetan Plateau:an initial study at Nam Co Lake. J Geophys Res-Atmos, 2018, 123(13): 6746-6759. DOI:10.1029/2018JD028330 |
| [9] |
Ren X, Wang YW, Zhang Z et al. Simulation studies for Lake Taihu effect on surrounding cities thermal environment. Acta Meteorologica Sinica, 2017, 75(4): 646-660. [任侠, 王咏薇, 张圳等. 太湖对周边城市热环境影响的模拟. 气象学报, 2017, 75(4): 645-660.] |
| [10] |
Lenters JD, Kratz TK, Bowser CJ. Effects of climate variability on lake evaporation:Results from a long-term energy budget study of Sparkling Lake, northern Wisconsin (USA). J Hydrol, 2005, 308(1-4): 168-195. DOI:10.1016/j.jhydrol.2004.10.028 |
| [11] |
Xiao K, Griffis TJ, Baker JM et al. Evaporation from a temperate closed-basin lake and its impact on present, past, and future water level. J Hydrol, 2018, 561: 59-75. DOI:10.1016/j.jhydrol.2018.03.059 |
| [12] |
Der Kamp GV, Keir D, Evans MS. Long-term water level changes in closed-Basin Lakes of the Canadian Prairies. Can Water Resour J, 2008, 33(1): 23-38. DOI:10.4296/cwrj3301023 |
| [13] |
Gal G, Imberger J, Zohary T et al. Simulating the thermal dynamics of Lake Kinneret. Ecol Model, 2003, 162(1-2): 69-86. DOI:10.1016/S0304-3800(02)00380-0 |
| [14] |
Eerola K, Rontu L, Kourzeneva E et al. A study on effects of lake temperature and ice cover in HIRLAM. Boreal Environ Res, 2010, 15: 130-142. |
| [15] |
Blanken PD, Spence C, Hedstrom NR et al. Evaporation from Lake Superior:1. Physical controls and processes. J Gt Lakes Res, 2011, 37(4): 707-716. DOI:10.1016/j.jglr.2011.08.009 |
| [16] |
Blanken PD, Rouse WR, Culf AD et al. Eddy covariance measurements of evaporation from Great Slave Lake, Northwest Territories, Canada. Water Resour Res, 2000, 36(4): 1069-1077. DOI:10.1029/1999WR900338 |
| [17] |
Wang W, Xiao W, Cao C et al. Temporal and spatial variations in radiation and energy balance across a large freshwater lake in China. J Hydrol, 2014, 511: 811-824. DOI:10.1016/j.jhydrol.2014.02.012 |
| [18] |
Wang B, Ma Y, Ma W et al. Physical controls on half-hourly, daily, and monthly turbulent flux and energy budget over a high-altitude small lake on the Tibetan Plateau. J Geophys Res-Atmos, 2017, 122(4): 2289-2303. DOI:10.1002/2016JD026109 |
| [19] |
Li Z, Lyu S, Zhao L et al. Turbulent transfer coefficient and roughness length in a high-altitude lake, Tibetan Plateau. Theor Appl Climatol, 2016, 124(3/4): 723-735. |
| [20] |
Subin ZM, Riley WJ, Mironov D. An improved lake model for climate simulations:Model structure, evaluation, and sensitivity analyses in CESM1. J Adv Model Earth Syst, 2012, 4(1): 183-204. |
| [21] |
Mironov D, Heise E, Kourzeneva E et al. Implementation of the lake parameterization scheme FLake into the numerical weather prediction model COSMO. Boreal Environ Res, 2010, 15: 218-230. |
| [22] |
Beletsky D, Schwab D, McCormick M. Modeling the 1998-2003 summer circulation and thermal structure in Lake Michigan. J Geophys Res, 2006, 111: C10010. DOI:10.1029/2005JC003222 |
| [23] |
Xue P, Schwab DJ, Hu S. An investigation of the thermal response to meteorological forcing in a hydrodynamic model of Lake Superior. J Geophys Res Oceans, 2015, 120: 5233-5253. DOI:10.1002/2015JC010740 |
| [24] |
Stepanenko VM, Goyette S, Martynov A et al. First steps of a Lake Model Intercomparison Project:LakeMIP. Boreal Environ Res, 2010, 15: 191-202. |
| [25] |
Stepanenko VM, Martynov A, Johnk KD et al. A one-dimensional model intercomparison study of thermal regime of a shallow, turbid midlatitude lake. Geoscientific Model Development, 2012, 5(4): 3993-4035. DOI:10.5194/gmdd-5-3993-2012 |
| [26] |
Thiery W, Martynov A, Darchambeau F et al. Understanding the performance of the flake model over the east-Africa great lakes. Geosci Model Dev, 2013, 7(1): 317-337. |
| [27] |
Xue P, Pal JS, Ye X et al. Improving the simulation of large lakes in regional climate modeling:Two-Way Lake-Atmosphere Coupling with a 3D Hydrodynamic Model of the Great Lakes. J Clim, 2017, 30(5): 1605-1627. DOI:10.1175/JCLI-D-16-0225.1 |
| [28] |
Gu H, Jin J, Wu Y et al. Calibration and validation of lake surface temperature simulations with the coupled WRF-lake model. Clim Change, 2015, 129(3/4): 471-483. |
| [29] |
Liu HP, Zhang Y, Liu S et al. Eddy covariance measurements of surface energy budget and evaporation in a cool season over southern open water in Mississippi. J Geophys Res, 2009, 114(D4). |
| [30] |
Liu HP, Blanken PD, Weidinger T et al. Variability in cold front activities modulating cool-season evaporation from a southern inland water in the USA. Environ Res Lett, 2011, 6(2): 024022. DOI:10.1088/1748-9326/6/2/024022 |
| [31] |
Rosenberry DO, Winter TC, Buso DC et al. Comparison of 15 evaporation methods applied to a small mountain lake in the northeastern USA. J Hydrol, 2007, 5(4): 149-166. |
| [32] |
Hu C, Wang Y, Wang W et al. Trends in evaporation of a large subtropical lake. Theor Appl Climatol, 2017, 129: 1-12. DOI:10.1007/s00704-016-1755-4 |
| [33] |
Wang W, Lee X, Xiao W et al. Global lake evaporation accelerated by changes in surface energy allocation in a warmer climate. Nat Geosci, 2018, 11(6): 410-414. DOI:10.1038/s41561-018-0114-8 |
| [34] |
Deng B, Liu S, Xiao W et al. Evaluation of the CLM4 Lake Model at a large and shallow freshwater lake. J Hydrometeorol, 2013, 14(2): 636-649. DOI:10.1175/JHM-D-12-067.1 |
| [35] |
Stepanenko VM, Johnk KD, Machulskaya E et al. Simulation of surface energy fluxes and stratification of a small boreal lake by a set of one-dimensional models. Tellus A, 2014, 66(1). |
| [36] |
Thiery W, Stepanenko VM, Xing F et al. LakeMIP Kivu:evaluating the representation of a large, deep tropical lake by a set of one-dimensional lake models. J Adv Model Earth Syst, 2016, 66(1): 21390. |
| [37] |
Lee X, Liu S, Xiao W et al. The Taihu Eddy Flux Network:An observational program on energy, water and greenhouse gas fluxes of a large freshwater lake. Bull Amer Meteorol Soc, 2014, 95(10): 1583-1594. DOI:10.1175/BAMS-D-13-00136.1 |
| [38] |
Garratt JR. The atmospheric boundary layer. New York: Cambridge University Press, 1992: 85-113.
|
| [39] |
Laird NF, Kristovich DAR. Variations of sensible and latent heat fluxes from a Great Lakes buoy and associated synoptic weather patterns. J Hydrometeorol, 2002, 3: 3-12. DOI:10.1175/1525-7541(2002)003<0003:VOSALH>2.0.CO;2 |
| [40] |
Foken T. The energy balance closure problem:An overview. Ecol Appl, 2008, 18(6): 1351-1367. DOI:10.1890/06-0922.1 |
| [41] |
Leuning R, Van Gorsel E, Massman WJ et al. Reflections on the surface energy imbalance problem. Agr Forest Meteorol, 2012, 156: 65-74. DOI:10.1016/j.agrformet.2011.12.002 |
| [42] |
Twine TE, Kustas WP, Norman JM et al. Correcting eddy-covariance flux underestimates over a grassland. Agric Forest Meteorol, 2000, 103(3): 279-300. DOI:10.1016/S0168-1923(00)00123-4 |
| [43] |
Wang W, Shen SH, Liu SD et al. Mechanistic analysis of the observed energy imbalance of Lake Taihu. Ecologica Sinica, 2017, 37(18): 5935-5950. [王伟, 申双和, 刘寿东等. 太湖生态系统能量闭合特征及其影响因素. 生态学报, 2017, 37(18): 5935-5950.] |
| [44] |
Zhang YL, Qin BQ, Chen WM et al. Analysis on distribution and variation of beam attenuation coefficient of Taihu Lake's water. Advances in Water Science, 2003, 14(4): 447-455. [张运林, 秦伯强, 陈伟民等. 太湖水体光学衰减系数的分布及其变化特征. 水科学进展, 2003, 14(4): 447-453. DOI:10.3321/j.issn:1001-6791.2003.04.011] |
| [45] |
Zhang Y, Qin B, Hu W et al. Temporal-spatial variations of euphotic depth of typical lake regions in Lake Taihu and its ecological environmental significance. Sci China:Ser D, 2006, 49(4): 431-442. DOI:10.1007/s11430-006-0431-4 |
| [46] |
Smith SD. Coefficients for sea surface wind stress, heat flux, and wind profiles as a function of wind speed and temperature. J Geophys Res, 1988, 93: 15467-15474. DOI:10.1029/JC093iC12p15467 |
| [47] |
Xiao W, Liu S, Wang W et al. Transfer Coefficients of Momentum, Heat and Water Vapor in the Atmospheric Surface Layer of a Large Freshwater Lake. Boundary-Layer Meteorology, 2013, 148(3): 479-494. DOI:10.1007/s10546-013-9827-9 |
| [48] |
Wang J, Bras RL. Ground heat flux estimated from surface soil temperature. J Hydrol, 1999, 216(3/4): 214-226. |
| [49] |
Wang M, Shi W, Tang J. Water property monitoring and assessment for China's inland Lake Taihu from MODIS-Aqua measurements. Remote Sens Environ, 2011, 115(3): 841-854. DOI:10.1016/j.rse.2010.11.012 |
 2019, Vol. 31
2019, Vol. 31 

