(2: 河海大学环境学院, 南京 210098)
(2: College of Environment, Hohai University, Nanjing 210098, P. R. China)
随着中国社会经济的快速发展,水污染问题日趋严重,东部平原河网地区尤为突出[1].近年来,国家和地方政府也纷纷出台了水污染防治、流域生态补偿等相关水环境政策、采取了一系列水污染治理措施,使水环境污染状况得到了一定的缓解,但污染仍在继续,整体水质情况依然不容乐观,因此,在以可持续发展为核心的环境保护新形势下,在水环境治理已有成效的基础上,更加积极探索新的治理思路和方法显得尤为重要.水污染物总量控制是改善水环境质量,实现经济、社会与环境可持续发展的根本途径之一,而制定科学的总量分配方案则是实施水污染物总量控制的关键技术[2].关于水污染物总量分配,国内外已有多位学者进行了深入研究.国外学者在进行水污染物总量分配技术研究过程中多是基于经济优化原则建立最优化数学模型,而我国对于水污染物总量分配的研究主要集中在以水环境容量或目标总量控制为基础,基于经济优化分配原则(即效率原则)或公平合理原则进行分配,主要有均等分摊允许纳污量、等比例削减现有排污量、区域内排污总量最小、区域内治理投资费用最小和公平分配允排量和削减量等方法[3].这些分配方法从实施效果看都存在不同程度的问题,使得环保机构尤其是基层环保机构没有一套合理有效的水污染物总量分配体系,难以将水污染物进行公平有效的分配,进而影响水环境治理可持续发展目标的实现.因此制定一套行之有效的水污染物总量分配方案迫在眉睫.
基尼系数是一种衡量收入与分配均衡程度的指标[4].基尼系数可以反映居民收入分配的不公平程度,已经成为表征国家或地区居民收入分配差距的一项重要指标[5].吴悦颖等[6]将其引入污染负荷分配并提出基于基尼系数的水污染负荷分配法,后续一些学者将该法用于水污染物总量分配,效果较好[7-9],但他们的研究仅是对基尼系数的单一应用,对于考虑不同指标对分配的重要性和影响程度以及各污染物分配区域的排污差距对分配的影响程度的研究较少.
本研究以典型平原河网地区张家港市为例,利用基尼系数理论综合考虑指标权重和区域贡献,建立一套全新的总量分配体系,将环境公平理论切实应用到污染物分配中,全面考虑各地区的污染现状、自然地理条件、经济发展状况、人口社会等多方面的客观因素,考量制定公平分配方案,以期为解决长期以来在污染物总量分配中难以权衡公平与效率的问题提供一种新的思路,促进新形势下水环境治理的可持续发展.
1 研究区域及方法 1.1 研究区域概况张家港市(31°43′12″~32°02′N,120°21′57″~120°52′E)地处长江三角洲发达地区,属太湖流域澄锡虞水系,境内河网密布,包括东中西部三大水系,拥有“一城四区”的城市框架,拥有2个国家级开发区,下辖8个镇、1个现代农业示范园区和1个双山岛生态旅游度假区.目前随着工农业生产和城市建设的高速发展,经济建设迅猛发展,但水资源配置不合理和水生态环境脆弱正逐步成为制约张家港市社会经济发展的主要因素.对《2015年度张家港市水功能区监测年报》分析可知,全市50 %左右的水体呈Ⅴ类及劣Ⅴ类,主要污染物为氨氮.基于对2015年各污染源的数据调查,进行统计计算后得出全年氨氮总排放量为2606.01 t.根据2015年张家港市年鉴提供的统计数据,研究区域常住人口125.31万人,土地面积为791.06 km2,GDP(地区生产总值)2229.82亿元.本研究涉及的区域范围包括金港镇、杨舍镇、锦丰镇、塘桥镇、凤凰镇、乐余镇、南丰镇、大新镇、农场(图 1).
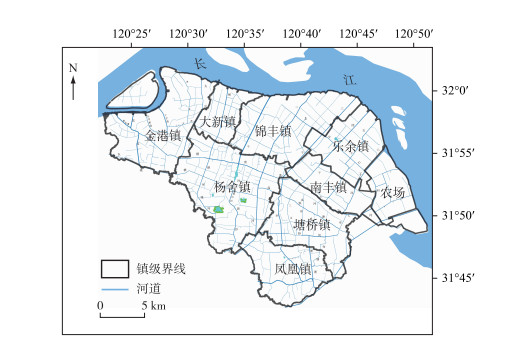
|
图 1 研究区域概况 Fig.1 Overview of the study areas |
采用一维降解模型的水动力和水质模块建立张家港市河网水动力和水质耦合数学模型,水动力模块计算采用圣维南方程组,采用“双扫”法进行数值计算,采用六点中心隐式差分格式.方程主要依据动量守恒和质量守恒,以水位和流量为变量,同时考虑了旁侧入流和漫滩的影响;水质模块是以水动力模型为基础,采用污染物对流扩散方程进行计算.根据河网概化原则[10],张家港市市镇级以上河道共概化为367条河流,151个闸站(图 2).
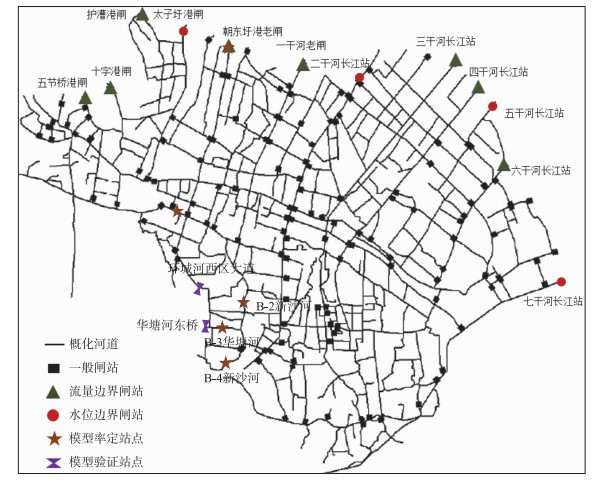
|
图 2 研究区域河网概化图 Fig.2 Generalization of the river network in the studied area |
模型上边界为五节桥港、十字港、护漕港、朝东圩港、一干河、三干河、四干河、六干河与长江交汇处,采用流量边界,流量数据来源于水文自动监测站输出频率为1 min的实时监测数据;模型下边界主要为太字圩港、二干河、五干河、七干河等与长江交汇处,均采用水位边界控制.
模型初始水位根据张家港市实际情况,设为常水位3.69 m.模型参数的设置采用2016年1月11—12日张家港市野外同步监测数据进行率定,模型验证采用2017年1月9—10日张家港市野外同步监测数据.
1.2.2 水环境容量计算根据1967—2013年共47年的张家港市多年月均降水量资料进行分析,计算得到90 %保证率下的枯水年(1971年)作为典型年,最低水位出现的2月份作为设计月份,基于河网水动力水质耦合模型水质综合降解系数率定结果,在设计流量条件下,以研究区域水功能区水质目标作为标准,采用总体达标法[11]计算出河网区每个河段的水环境容量,汇总得到研究区域各乡镇水体水环境容量.
1.2.3 贡献系数贡献系数是指地区评价指标(人口、土地面积、GDP或环境容量)贡献率与污染物排放量贡献率的比值,计算公式[12]为:
| $ C C_{j}=\left(M_{i j} / M_{j}\right) /\left(W_{i} / W\right) $ | (1) |
式中,CCj为基于指标j的贡献系数,当指标j为人口、土地面积、GDP和环境容量时,CCj分别代表人口贡献系数、土地面积贡献系数、经济贡献系数(又称绿色贡献系数GCC)和水环境容量贡献系数;Mij为第i个行政分区指标j的值,Mj为研究区域指标j的值,Mij/Mj为第i个行政分区指标j的贡献率,Wi为第i个行政分区的污染物排放量,W为研究区域污染物排放总量,Wi/W为第i个行政分区污染物排放量的贡献率.
若CCj>1,表明指标j的贡献率大于污染物排放贡献率,相对较公平;若CCj < 1,表明污染排放贡献率大于指标j的贡献率,存在不公平现象,CCj值越小越不公平.环境基尼系数反映在一定单元内部污染负荷分配的内部公平性,而贡献系数表现的是控制单元间的外部影响,可作为分辨外部公平性的依据[13].
1.2.4 水污染物总量公平分配模型构建1) 环境基尼系数:环境基尼系数延续了基尼系数注重“均衡性和差异性”的评估特性,在评估污染物分配方案上也体现了多元公平性原则[14].本研究参考多数学者以及经济发展水平相似的东部平原河网地区的研究成果,将环境基尼系数的合理范围设置为0~0.2[12, 15-16].
2) 环境基尼系数评价指标的筛选:影响水污染物总量分配的因素主要有人口、资源、经济和水污染物承受能力4个方面[17],每个因素均涉及到较庞大的具体指标体系,部分指标存在数据统计不全或难于统计等问题,且每个因素之间都存在着千丝万缕的关系,为使操作方法在今后环境管理与污染物控制中便于实施,在各因素具体指标选择时应选择数据具有典型性、易采集、易定量化,具有比较性的指标.遂将环境基尼系数评价指标择定为人口、土地面积、GDP和环境容量,各项指标分别作为代表 4大影响因素的关键因子,其中人口、土地面积及GDP数据均来源于《2015年张家港统计年鉴》[18],环境容量根据模型水质综合降解系数率定结果,采用总体达标法计算得到.
3) 单因子环境基尼系数的计算:以研究区域行政分区为基本单元计算环境基尼系数,将各乡镇单位各指标所承载的污染负荷按递增形式排序,计算各乡镇各指标累积比例和污染负荷累积比例,以各指标累积比例为横坐标,以污染负荷累积比例为纵坐标,绘制洛伦兹曲线图,采用梯形面积法[19]进行计算:
| $ G_{j}=1-\sum\limits_{i=1}^{m}\left(X_{i j}-X_{(i-1) j}\right)\left(Y_{i}+Y_{i-1}\right) $ | (2) |
式中,i为乡镇编号;j为指标编号;m为乡镇数;Gj为基于指标j的基尼系数;Xij为第i个乡镇指标j的累积比例(%);Yi为第i个乡镇排放或分配污染物量的累积比例;当i=1时,X(i-1)j=0,Yi-1=0.
4) 指标权重:水污染物总量分配涉及到多个指标基尼系数的调整,而不同指标对分配的重要性和影响程度是不相同的,因此考虑为各指标分配权重,采用熵值法[9]计算指标权重,综合所有指标的基尼系数作为一个整体进行调整,计算公式为:
| $ P_{i j}=\frac{W_{0(i)}}{Z_{i j}} $ | (3) |
| $ N_{i j}=\frac{P_{i j}}{\sum _{j=1}^{m} P_{i j}} $ | (4) |
| $ E_{j}=\frac{1}{\ln m}-\sum\limits_{j=1}^{m}\left(N_{i j} \cdot \ln N_{i j}\right) $ | (5) |
| $ V_{j}=\frac{1-E_{j}}{\sum _{j=1}^{n} E_{j}} $ | (6) |
式中,W0(i)为各污染物分配单元i中的污染物现状入河排放量;Zij为各污染物分配单元i中评价指标j的值;Pij为各污染物分配单元i中评价指标j的单位污染物现状入河排放量;Nij为评价指标j下各污染分配单元i中的评价指标j值在该评价指标j中所占比重;Ej为评价指标j单位污染物现状入河排放量的信息熵;Vj为环境基尼系数评价指标j的权重;n为环境基尼系数评价指标j的个数.
5) 熵值—环境基尼系数最小化模型:以各指标基尼系数总和最小为目标函数,研究区域内各乡镇水污染物分配的排放量为决策变量,考虑污染物总量削减目标、各指标现状环境基尼系数以及各乡镇污染物削减比例上、下限等约束条件,利用Matlab工具软件对模型进行优化求解,确定最终的最优分配方案.主要计算公式为:
目标函数:
| $ \min G=\sum\limits_{j=1}^{n} V_{j} \cdot G_{j} $ | (7) |
总量削减约束:
| $\sum\limits_{i=1}^{m} W_{i}=(1-q) \sum\limits_{i=1}^{m} W_{0(i)} $ | (8) |
各指标优化后的环境基尼系数约束:
| $ G_{j} \leqslant G_{0(j)} $ | (9) |
各乡镇污染物削减比例约束:
| $ W_{i}=\left(1-P_{i}\right) W_{0(i)} $ | (10) |
| $ P_{i 0} \leqslant P_{i} \leqslant P_{i 1} $ | (11) |
式中,G为各指标基尼系数的总和;Gj为优化后指标j基尼系数;Vj为指标j权重;G0(j)为指标j基尼系数现状值;W0(i)为第i个乡镇污染负荷现状值;q为目标总量削减率;Pi为优化后第i个乡镇的污染物削减率;Pi0为第i个乡镇的削减率下限,Pi1为第i个乡镇的削减率上限.
2 结果与讨论 2.1 模型率定验证结果根据2016年1月11—12日与2017年1月9—10日张家港市野外同步监测数据对建立的河网水动力水质耦合模型,采用试错法进行率定验证(图 3,图 4).结果表明:模型计算结果与野外监测值模拟较好,流量相对误差在20 %以内,水质相对误差在30 %以内,符合模拟精度要求.氨氮降解系数设为0.03~0.08 d-1.
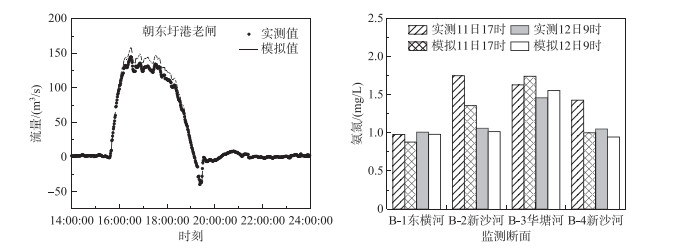
|
图 3 河网水动力水质耦合模型率定结果 Fig.3 Calibration results of the hydrodynamic and water quality model of river network |
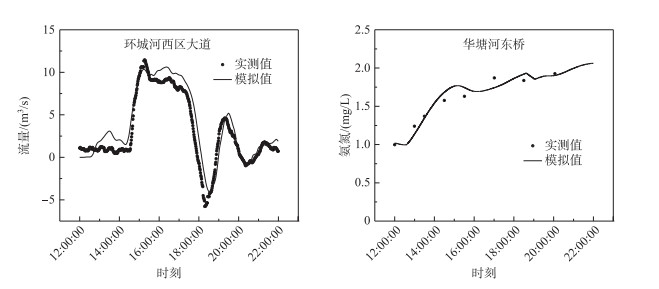
|
图 4 河网水动力水质耦合模型验证结果 Fig.4 Validation results of the hydrodynamic and water quality model of river network |
根据张家港市2015年现状水质调查情况,氨氮超标率最高(接近40 %),为主要污染物.为满足区域水环境管理要求,选取氨氮作为本研究水环境容量的计算因子.基于河网水动力水质耦合模型水质综合降解系数率定结果,利用总体达标计算法得出张家港市各省、市级水环境功能区及功能区外主要河道水环境容量,最后汇总得到研究区域内各个乡镇的水环境容量(表 1).
| 表 1 张家港市各乡镇水环境容量计算结果 Tab. 1 Water environmental capacity of towns in Zhangjiagang City |
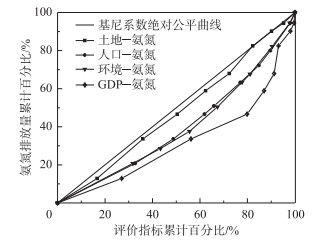
排污现状公平性分析是实行基于公平性原则的水污染物总量分配的前提,利用环境基尼系数可反映分配不公平程度的特性[20],可作为评价张家港市水污染物总量分配公平性的重要判据.以张家港市9个乡镇为基本统计单元,以主要污染物氨氮为控制目标,选取人口、土地面积、水环境容量、GDP为评价指标,基于环境基尼系数评价张家港市排污现状的公平性.各评价指标的现状环境基尼系数见表 2,基于各评价指标的洛伦兹曲线见图 5.结果表明:基于土地面积—氨氮污染负荷的环境基尼系数低于0.2,分配处于合理范围内,在4项指标中最小,说明从自然资源角度看,张家港市氨氮污染物排放较均衡;而基于人口—氨氮污染负荷、水环境容量—氨氮污染负荷和GDP—氨氮污染负荷的环境基尼系数均超过警戒线0.2,说明从人口、水体污染物承受能力和经济角度看,张家港市不同地区的氨氮污染物排放不够均衡,存在不公平现象,需要进行优化分配.
| 表 2 张家港市基于各评价指标的环境基尼系数 Tab. 2 The environmental Gini coefficient in Zhangjiagang Ctiy |
|
图 5 张家港市各指标氨氮污染负荷洛伦兹曲线 Fig.5 Lorenz curves of the ammonia nitrogen pollutant in Zhangjiagang City |
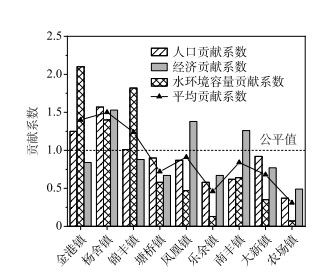
环境基尼系数能反映不同地区排污差距的大小,而通过对贡献系数的计算能进一步掌握排污差距的构成特点,弄清张家港市各乡镇对总体差距的贡献,甄别造成排污差距的主要不公平污染物分配单元,为后续评价总量优化分配方案的合理性提供参考依据[21].选取环境基尼系数超过警戒线的人口、水环境容量以及GDP 3个指标,分别计算张家港市各乡镇的贡献系数(图 6).从氨氮人口贡献系数计算结果可知,金港镇、杨舍镇和锦丰镇的氨氮人口贡献系数均大于1,说明这些地区人均排污量较小,而其他乡镇氨氮人口贡献系数均小于1,故这些乡镇是引起不公平的主要污染物分配单元;从氨氮水环境容量贡献系数分析,金港镇、杨舍镇和锦丰镇的氨氮水环境容量贡献系数均大于1,表明这3个地区单位环境容量排污量较小,没有超过单位水体污染物承受能力,其中金港镇的氨氮水环境容量贡献系数达到了2.1,在各乡镇中最大,说明了金港镇的单位环境容量排污量与单位水体污染物承受能力相适性较好.而凤凰镇、乐余镇、大新镇、农场的氨氮水环境容量贡献系数均小于1,故这4个乡镇是引起不公平的主要污染物分配单元,其中乐余镇和农场的氨氮水环境容量贡献系数较小,分别为0.13和0.07,说明这两个地区单位水环境容量排污量较大,在引起不公平的主要污染物分配单元中应重点考虑;从氨氮经济贡献系数分析,杨舍镇、凤凰镇、南丰镇的氨氮经济贡献系数均大于1,说明这些地区在发展经济的同时也考虑到了水环境保护,在一定程度上控制了污染物排放量,表现为绿色发展模式,其中,杨舍镇的氨氮经济贡献系数最大,表明该地区的单位GDP排污量与经济发展相适性最好,而其他乡镇氨氮经济贡献系数均小于1,说明这些地区是引起不公平的主要污染物分配单元.
|
图 6 张家港市各乡镇贡献系数对比 Fig.6 Contrast of the contribution coefficient of towns in Zhangjiagang City |
将各乡镇按氨氮平均贡献系数排序为杨舍镇>金港镇>锦丰镇>凤凰镇>南丰镇>塘桥镇>大新镇>乐余镇>农场.
2.4 张家港市水污染物总量优化分配为响应生态环境保护要求同时保证分配方案的可实施性,综合考虑张家港市氨氮水环境容量、现状排放量、区域经济发展水平以及实际承受能力,确定到“十三五”末,全市氨氮污染物总量削减目标为25 %,各乡镇总量削减上下限设为30 %、1 %.
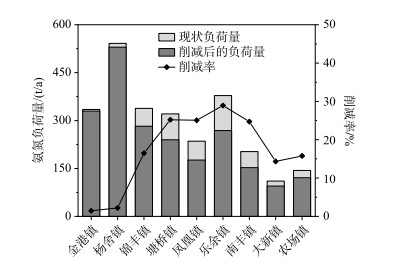
根据环境基尼系数最小化模型,计算得到优化后的环境基尼系数(表 2),进一步得到在人口、土地面积、水环境容量和GDP环境基尼系数总和最小且4项指标都小于现状值的情况下,张家港市各乡镇氨氮污染负荷的分配方案(图 7).结果表明:各项指标环境基尼系数优化后都有不同程度地减小,但总环境基尼系数降幅并不大,下降了0.0934(-11.2 %),更趋于合理和公平.环境基尼系数降幅最大的指标是GDP,下降了0.0429(-11.9 %).降幅最小的是人口对应的环境基尼系数,下降了0.0128(-6.1 %).优化后的环境基尼系数并未全部低于警戒线0.2,这与削减率的上、下限约束以及削减总量有关,削减率上、下限设置越宽,削减总量越大,环境基尼系数降幅就越大,但总量控制应遵循“循序渐进、逐步改善”的原则,削减总量与削减率上、下限要根据区域排污状况、污染物控制指标、环境保护规划和实际承受能力等确定,不能为了追求环境基尼系数降低而不切实际地将污染负荷一次性削减到位[21].
|
图 7 张家港市各乡镇氨氮分配方案 Fig.7 The allocation scheme of ammonia nitrogen of towns in Zhangjiagang City |
氨氮排放量削减比例排序为乐余镇>塘桥镇>凤凰镇>南丰镇>锦丰镇>农场>大新镇>杨舍镇>金港镇.
2.5 污染物优化分配方案讨论基于基尼系数的污染物目标总量分配方法是以公平性为原则,能合理地将污染物分配到各个行政单元, 已成功应用于巢湖、松花江、海河流域、汤逊湖等流域污染物分配研究,研究结果都呈现了相同的规律:
1) 污染物削减比例的大小和污染物现状排放量之间并不具有一致性,即最终的分配方案并非污染物排放量大的乡镇污染物削减比例一定大.本研究中优化后的氨氮分配方案,氨氮排放量削减比例排序为乐余镇>塘桥镇>凤凰镇>南丰镇>锦丰镇>农场>大新镇>杨舍镇>金港镇,而氨氮现状排放量为杨舍镇>乐余镇>锦丰镇>金港镇>塘桥镇>凤凰镇>南丰镇>农场>大新镇,污染物削减比例的大小和污染物现状排放量之间并不具有一致性,最终的分配方案是综合考虑各乡镇的人口、资源、经济和水污染物承受能力等多方面的客观因素,经过熵值—环境基尼系数法优化分配后得到的相对最为公平的分配方案.比如杨舍镇是张家港市氨氮排放总量最大的区域,但人口、土地面积等也是张家港市最多的乡镇,经济也较发达,故综合考虑它对张家港市的总体贡献,最终削减比例仅为2.21 %,略高于金港镇,这与杨舍镇平均贡献系数最大的结果基本相一致,即平均贡献系数大的地区需削减的污染负荷少一些,而平均贡献系数小的地区(主要不公平分配单元)需削减的污染负荷相对多一些.
2) 优化后的基尼系数并未全部低于警戒水平,这与削减总量,削减率上、下限约束,以及分配模型目标函数的设计有关.削减总量越大,削减率上、下限设置越宽,基尼系数削减幅度就越大.但是总量控制应遵循“循序渐近、逐步改善”的原则,削减总量和削减率上、下限要根据区域排污状况、污染控制目标、环境保护规划和实际承受能力等确定,不能为了追求基尼系数降低而不切实际地将污染负荷一次性削减到位.
3 结论1) 张家港市各乡镇基于人口、水环境容量和GDP的氨氮污染负荷现状环境基尼系数分别为0.2096、0.2173和0.3608,均超出了环境基尼系数的合理范围(0~0.2),存在着不公平现象,亟待优化.各乡镇的平均贡献系数结果表明乐余镇和农场的不公平性特征最突出.
2) 通过熵值—环境基尼系数最小化模型,可实现张家港市各乡镇2020年氨氮排放量的优化分配,氨氮排放量削减比例排序为乐余镇>塘桥镇>凤凰镇>南丰镇>锦丰镇>农场>大新镇>杨舍镇>金港镇.
3) 在水污染物总量分配过程中,污染物削减比例的大小和污染物现状排放量之间并不具有一致性,即污染物排放量大的分配单元污染物削减比例不一定大,最终的分配方案要综合考虑多方因素确定.论文构建的熵值—环境基尼系数最小化模型综合考虑了研究区域社会、经济、资源等多种客观因素,对于平原河网地区,由于其特殊的地理位置和自然条件,人口、资源等分布相对比较均匀,故基于该模型所得到的分配方案充分表现了多元公平性原则,更公平合理.
4) 水污染物总量公平分配模型适用于指标分布相对较均匀的平原地区,包括湖泊、河网等,但分配各方必须是同一层面、具有可比性的对象,如流域与行政区之间就无法统一分配,分配对象的层面不一致会导致其属性有很大的差别,基尼系数可能会出现强烈的偏差.基于综合环境基尼系数最小化模型的目标总量分配最优化求解,跟以往只用基尼系数来判断总量分配方案是否合理的做法相比,保证了在一定约束条件下分配方案的最优性,使分配结果更加合理.
| [1] |
Xu YX, Wang WC, Zeng WF et al. Simulation on improvement of water environment in plain river network by water diversion. Water Resources Protection, 2018, 34(1): 70-75, 82. [许益新, 王文才, 曾伟峰等. 调水引流改善平原河网水环境质量模拟. 水资源保护, 2018, 34(1): 70-75, 82.] |
| [2] |
Zhao Q, Wang WP, Yang YJ et al. Review of study on total amount allocation of water pollutants in river and marine. China Population Resources and Environment, 2014, 24(S1): 82-86. [赵骞, 王卫平, 杨永俊等. 河流和海洋污染物总量分配研究述评. 中国人口·资源与环境, 2014, 24(S1): 82-86.] |
| [3] |
Meng XM. The application ofgini coefficient in total water waste load allocation[Dissertation]. Tianjin: Tianjin University, 2007. [孟祥明.基尼系数法在水污染物总量分配中的应用[学位论文].天津: 天津大学, 2007. ]
|
| [4] |
Ma YH, Niu J, Liu HL. Analysis of gini coefficient of water resources in Shanxi Province based on multiple perspectives. Journal of Shanxi Normal University:Natural Science Edition, 2019, 33(2): 100-105. [马艳红, 牛娟, 刘海龙. 基于多角度的山西省水资源基尼系数分析. 山西师范大学学报:自然科学版, 2019, 33(2): 100-105.] |
| [5] |
Chen S, Yu LJ, Wan HY et al. Case study of watershed pollution load distribution based on coupling model. South-to-North Water Transfers and Water Science & Technology, 2019, 17(5): 108-114. [陈帅, 于鲁冀, 万红友等. 基于耦合模型的流域污染负荷分配实例. 南水北调与水利科技, 2019, 17(5): 108-114.] |
| [6] |
Wu YY, Li YS, Liu WJ. Study ongini coefficient method of total pollutant load allocation for water bodies. Research of Environmental Sciences, 2006, 19(2): 66-70. [吴悦颖, 李云生, 刘伟江. 基于公平性的水污染物总量分配评估方法研究. 环境科学研究, 2006, 19(2): 66-70. DOI:10.13198/j.res.2006.02.80.wuyy.016] |
| [7] |
Wang Y, Niu ZG, Wang W. Application of gini coefficient in total waste load district allocation for surface-water. China Population Resources and Environment, 2008, 18(3): 177-180. [王媛, 牛志广, 王伟. 基尼系数法在水污染物总量区域分配中的应用. 中国人口·资源与环境, 2008, 18(3): 177-180. DOI:10.3969/j.issn.1002-2104.2008.03.034] |
| [8] |
Xiao WH, Qin DY, Li W et al. Model for distribution of water pollutants in a lake basin based on environmental Gini coefficient. Acta Scientiae Circumstantiae, 2009, 29(8): 1765-1771. [肖伟华, 秦大庸, 李玮等. 基于基尼系数的湖泊流域分区水污染物总量分配. 环境科学学报, 2009, 29(8): 1765-1771. DOI:10.13671/j.hjkxxb.2009.08.028] |
| [9] |
Li RZ, Shu K. Fuzzy optimization model for waste load allocations based on the Gini coefficient. Acta Scientiae Circumstantiae, 2010, 30(7): 1518-1526. [李如忠, 舒琨. 1526基于基尼系数的水污染负荷分配模糊优化决策模型. 环境科学学报, 2010, 30(7): 1518-1526. DOI:10.13671/j.hjkxxb.2010.07.022] |
| [10] |
Yang SB, Dong ZY. Study on the influence of river network generalized density to hydrodynamic model for plain river system. Journal of Zhejiang University of Technology, 2007, 35(5): 567-570. [杨松彬, 董志勇. 河网概化密度对平原河网水动力模型的影响研究. 浙江工业大学学报, 2007, 35(5): 567-570. DOI:10.3969/j.issn.1006-4303.2007.05.023] |
| [11] |
Code of practice for computation on allowable permitted assimilative capacity of water bodies, 2010. [水域纳污能力计算规程, 2010. ]
|
| [12] |
Wang JN, Lu YT, Zhou JS et al. Analysis of China resource-environment Gini coefficient based on GDP. China Environmental Science, 2006, 26(1): 111-115. [王金南, 逯元堂, 周劲松等. 基于GDP的中国资源环境基尼系数分析. 中国环境科学, 2006, 26(1): 111-115. DOI:10.3321/j.issn:1000-6923.2006.01.024] |
| [13] |
Wu WJ, Jiang HQ, Duan Y et al. Application of total water pollutant load distribution in control-unit based on the environmental Gini coefficient. China Population Resources and Environment, 2017, 27(5): 8-16. [吴文俊, 蒋洪强, 段扬等. 基于环境基尼系数的控制单元水污染负荷分配优化研究. 中国人口·资源与环境, 2017, 27(5): 8-16. DOI:10.12062/cpre.20170307] |
| [14] |
Zhong XH, Wang FE, Yu J et al. Application of WASP model and gini coefficient in the total amount control of water pollutant:A case study in Tiaoxi Estuary of South Taihu Lake. Journal of Zhejiang University:Sciences Edition, 2015, 42(2): 181-188. [钟晓航, 王飞儿, 俞洁等. 基于WASP水质模型与基尼系数的水污染物总量分配——以南太湖苕溪入湖口区域为例. 浙江大学学报:理学版, 2015, 42(2): 181-188.] |
| [15] |
Liu Y, Wu RH, Liao RX. Study of equity evaluation of total load allocation for atmosphere pollutants. Environmental Science and Management, 2007, 23(9): 159-162. [刘耀, 吴仁海, 廖瑞雪. 大气污染物总量分配公平性评价研究. 环境科学与管理, 2007, 23(9): 159-162. DOI:10.3969/j.issn.1673-1212.2007.09.048] |
| [16] |
Xie G, Peng YB, Li BC et al. A comparative study on water pollution control between TMDL and small river basin pollution comprehensive treatment-example as water pollution treatment in Shandong Province during south water to north. Journal of Agricultural Mechanization Research, 2006, 28(5): 189-192. [谢刚, 彭岩波, 李必成等. TMDL计划与小流域污染综合治理思路的研究——以南水北调东线山东段治污为例. 农机化研究, 2006, 28(5): 189-192. DOI:10.3969/j.issn.1003-188X.2006.05.066] |
| [17] |
Tian P, Fang XB, Wang FE et al. Use of a minimum environmental Gini Coefficient model on optimizing the allocation plan of total pollutant load in water bodies:A case study at Zhangjiagang river-network plain. China Environmental Science, 2014, 34(3): 801-809. [田平, 方晓波, 王飞儿等. 基于环境基尼系数最小化模型的水污染物总量分配优化——以张家港平原水网区为例. 中国环境科学, 2014, 34(3): 801-809.] |
| [18] |
The statistical yearbook of Zhangjiagang in 2015, 2015. [2015年张家港统计年鉴, 2015. ]
|
| [19] |
Jacobson A, Milman AD, Kammen DM. Letting the (energy) Gini out of the bottle:Lorenz curves of cumulative electricity consumption and Gini coefficients as metrics of energy distribution and equity. Energy Policy, 2005, 33(14): 1825-1832. DOI:10.1016/j.enpol.2004.02.017 |
| [20] |
Liu Q, Li Z, Yao G. Fairness of total water pollutants load allocation based ongini coefficient method. China Water & Wastewater, 2016, 32(11): 90-94. [刘奇, 李智, 姚刚. 基于基尼系数的水污染物总量分配公平性研究. 中国给水排水, 2016, 32(11): 90-94.] |
| [21] |
Qin DL, Wei AL, Lu SY et al. Total water pollutant load allocation in dongting lake area based on the environmental gini coefficient method. Research of Environmental Sciences, 2013, 26(1): 8-15. [秦迪岚, 韦安磊, 卢少勇等. 基于环境基尼系数的洞庭湖区水污染总量分配. 环境科学研究, 2013, 26(1): 8-15. DOI:10.13198/j.res.2013.01.12.qindl.006] |
 2020, Vol. 32
2020, Vol. 32 

