洞庭湖是我国第二大淡水湖,是调节湘、资、沅、澧四水和分蓄长江洪水重要的天然湖泊,为长江流域重要的调蓄湖泊和水源地,对整个长江中游的防洪和水资源利用举足轻重,同时洞庭湖也是世界著名的湿地生态保护地区,对区域生态系统的维护和生物多样性的保护具有重要作用[1].然而,由于气候变化以及人类活动等多种因素,湿地面积不断萎缩,湖泊湿地生态系统也造成较大破坏[2].湖泊水位情势变化是决定湖泊生态系统的重要影响因素,其时空变化过程对湖泊生态系统安全产生深远影响.因此,确定湖泊生态水位,对于恢复湖泊生态系统功能以及维护湖泊健康可持续发展具有重要研究意义.
关于湖泊生态水位,国内外学者开展了大量研究.国外生态水位研究起源于美国,其中Zacharias等2005年运用MIKESHE软件、遥感和GIS等手段对Trichonis湖泊湿地的生态需水和生态水位变化进行了估算[3]. Desgranges等2006年研究了湿地鸟类和水位之间的动态响应关系,运用生态统计方法和构建模型估算出适合鸟类繁衍的水位[4]. Hudon等2006年运用综合模拟方案研究了湖泊水位与植物之间的关系,确定了适合植被生长的生态水位[5].我国研究湖泊生态水位相对较晚,其中崔保山等2005年基于生态水文学原理提出了计算最小生态需水量的3种方法:曲线相关法、功能法和最低生态水位法[6].李新虎等2007年运用综合指标法计算分析了博斯腾湖最低生态水位[7].淦峰等2015年提出湖泊生态水位包括水位变化范围和过程,通过构建高低水位发生时间、持续时间和水位变化率等生态水位指标体系,确定了鄱阳湖生态水位目标值的范围[8].已有一些关于洞庭湖生态水位的相关研究.谢永宏等2012年计算分析了洞庭湖1974、1988和1998年3个时期城陵矶水文站最小生态水位分别是24、24和24.6 m[9].梁婕等2013年对东洞庭湖城陵矶水文站拟合水文变异前月均水位序列的最适合概率分布函数,认为概率最高处的月均水位为生态水位(24.90 m)[10].程俊翔等2015年采用最低年平均水位法、年保证率设定法、湖泊形态分析法和生态水位法计算东洞庭湖最低生态水位为25.42 m[11].根据目前相关研究,发现湖泊生态水位计算方法主要包括天然水位资料法、湖泊形态分析法和生物空间最小需求法,这些方法大多计算一个最低生态水位,忽略了湖泊的年内水位变化过程,实际上湖泊中水生生物在不同生长阶段对湖泊水位的需求也不相同,多样化的水位情势变化,同时也增加了水生生物多样性.
考虑到湖泊生态系统的复杂性和多样性,笔者认为湖泊生态水位是指维持湖泊生态系统结构功能完整性所需的水位,包括水位的变化范围和过程.为了计算方便,通常将湖泊生态水位分为最小和适宜生态水位进行计算,其中湖泊最小生态水位是维持湖泊生态系统生物物种不消亡、湖泊生态系统的健康以及基本功能不严重退化所需要保持的最低水位;适宜生态水位是指维持湖泊生态系统结构稳定和生物多样性不受损所需的最适宜水位.本文针对洞庭湖湖泊水文变异情况,提出了一种计算湖泊生态水位的水文学新方法,该方法将年内展布法[12]与IHA-RVA法[13]进行结合,分别计算湖泊最小和适宜生态水位,并分析了水文变异前后生态水位保障程度,提出了洞庭湖生态水位保障措施,该研究为洞庭湖湿地健康恢复提供了理论依据.
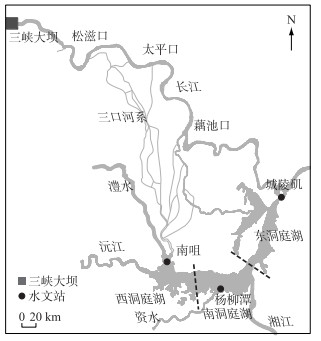
1 研究数据和方法 1.1 研究区域及数据来源洞庭湖位于湖南省北部,跨湘、鄂两省,是我国第二大淡水湖泊.洞庭湖西高东低,被分为东洞庭湖(城陵矶)、南洞庭湖(杨柳潭)、西洞庭湖(南咀),自西向东形成一个倾斜的水面(图 1).
|
图 1 洞庭湖示意图 Fig.1 Sketch map of Lake Dongting |
洞庭湖作为长江中下游最为典型的吞吐型湖泊,不但有着蓄水防洪的作用,同时也是世界公认的重要湿地保护区.洞庭湖优越的地理位置以及良好的生态环境,使其在我国水生态保护区中有着举足轻重的地位,在维护生物多样性、旅游观光以及水资源调度中发挥着巨大的生态效益、经济效益和社会效益.作为世界级湿地生态保护区洞庭湖湿地每年有大量的珍稀候鸟在此越冬,有国家一级保护动物13种,包括白鹤、白头鹤、白鹳、黑鹳、大鸨、中华秋沙鸭、东方白鹳、黑鹳、白尾海雕、白鹤、白头鹤、大鸨、游隼,二级保护动物天鹅、白琵鹭、鸿雁等35种.同时也有国家Ⅰ级保护植物水杉、银杏和Ⅱ级保护植物翠柏、马蹄参、野大豆、八角莲等30种珍稀植物,另外洞庭湖湿地也是长江四大家鱼重要产卵地之一和国家一级保护鱼类中华鲟、白鲟等珍稀濒危水生动物的保护地[1].近年来,由于气候变化以及人类活动等多因素影响,洞庭湖水系调蓄功能衰退、生态环境逐渐恶劣、生物多样性及水生生物的生存繁殖面临严峻的挑战.这就使得对洞庭湖湿地进行科学合理的水文水生态研究迫在眉睫.本文选取分别代表东洞庭湖、南洞庭湖和西洞庭湖的3个代表水文站城陵矶、杨柳潭、南咀的日均水位为研究对象,3个代表水文站日均水位数据序列为1959—2016年,数据来源于湖南省水利水电勘察设计研究总院.
1.2 趋势分析及突变检验Mann-Kendall(M-K)趋势检验通过计算时间序列数据的标准化变量Z,与某一置信水平α(取0.05)下的临界变量对比.当Z为正表示有上升趋势,为负则表示有下降趋势;当Z超临界值时表明上升或下降趋势显著,同时对原时间序列的逆序列进行同样的统计量计算,使UB=-UF,若两条曲线在95 %置信度水平内出现交点,表明在该时间点发生突变[14]. M-K非参数检验不受样本值和分布类型的干扰,但是检验过程中可能出现多个突变点,需要对这些突变点进行验证.累积距平法是年均水文数据和多年年均水文数据之间差值的累积值,选取累积量存在的极值点为水文突变点[15].滑动T检验法是通过计算T统计量,观察T统计量是否超过显著水平线,若超过了显著水平线,则表示该时间点为水文突变点[16]. 3种算法应用较为广泛和普遍,本文不再做详细介绍,具体算法参见参考文献[14-16].依据3种算法的计算结果和实测历史水位数据确定洞庭湖水文变异的时间点,并依次划分水文分析的基准期和评价期.
1.3 生态水位计算方法湖泊水文过程具有周期性变化规律,并伴随着相应的生态系统响应与特定的生态作用.湖泊水生生物的生命史已经适应湖泊的天然水文情势,湖泊生态系统处于相对平衡状态.而天然最小月均水位能够满足湖泊基本生态环境功能、水生生物生存及群落结构对水量的基本需求,天然适宜生态水位为能够保持湖泊生态系统结构稳定的适宜水位[12, 17].然而,由各月最小月均水位和适宜生态水位构成的年内过程不能很好地反映出河流的水文特征,而湖泊多年月均水位过程能够更好地反映出湖泊历史水文情势变化特征.因此,本研究认为湖泊生态水位计算方法应该基于湖泊天然径流过程的自身特征来进行确定与量化水文指标,并结合多年条件下的同期平均径流进行生态水位计算,即基于长时间序列的天然月均水位资料,选取多年年均水位与年内各月最小(适宜)月均水位的年均值这两个典型的水文特征变量确定与量化关键水文指标——同期均值比,并结合典型年水位过程或多年平均水位过程进行湖泊内生态标准水位的年内过程计算.
首先,根据上述水文变异的计算结果,运用突变前的天然水位资料,分别计算多年平均水位和最小年均水位;其次,利用多年年均水位和最小年均水位,计算各水文断面的同期均值比;然后,分析历史湖泊天然水位过程,利用历史水位资料构建多年月平均水位的年内过程,结合同等比例缩放的原理进行湖泊生态水位计算,得到各控制断面的最小生态水位年内过程.计算公式为[12]:
| $ \left\{ {\begin{array}{*{20}{l}} {\bar Z = \frac{1}{{12}}\sum\limits_{i = 1}^{12} {{{\bar z}_i}\;\;\;\;\;\;\;\;\;\;其中\;{{\bar z}_i} = \frac{1}{n}\sum\limits_{j = 1}^n {{{\bar z}_{ij}}} } }\\ {{{\bar Z}_{\min }} = \frac{1}{{12}}\sum\limits_{i = 1}^{12} {{z_{\min (i)}}} {\rm{ 其中 }}{z_{\min \left( i \right)}} = \min \left( {{z_{ij}}} \right),\;j = 1,2, \cdots n}\\ {\eta = {{\bar Z}_{\min }}/\bar Z}\\ {{Z_i} = {{\bar z}_i} \cdot \eta } \end{array}} \right. $ | (1) |
式中,Z为多年年均水位,Zmin为最小年均水位,i为第i个月的多年平均水位,zmin(i)为第i个月的多年最小水位,zij为第j年第i个月的月均水位,n为统计年数,η为同期均值比,zi为各月的最小生态水位.
在计算最小生态水位过程基础上,采用IHA-RVA法计算湖泊适宜生态水位,其计算原理考虑到湖泊适宜生态水位变动范围不应超过天然可变范围(即RVA阈值),这样才能够维持湖泊健康生态系统. RVA阈值描述水位过程线的可变范围,也即天然生态系统可以承受的变化范围,这为估算湖泊生态水位系列提供了参考.我们以各指标的平均值(标准差)或者以频率为75 %和25 %作为各个指标的上下限,称为高低水位阈值,研究以下限水位的年均值作为适宜年均水位(等同于最小生态水位计算公式中的最小年均水位)[13, 18-19].基于长时间序列的天然日均水位资料,选取多年年均水位和适宜年均水位这两个典型的水文特征变量进行确定与量化关键水文指标——同期均值比,并结合多年平均水位过程进行湖泊内适宜生态水位的年内过程计算,计算步骤与公式(1)类似.
1.4 生态水位保障度根据计算的最小和适宜生态水位,进行湖泊生态水位保障度计算[20].生态水位保障度即计算时段内,湖泊水位能够保障生态水位的天数与总天数的比值.该值越大,表明该时段水位越能够保障湖泊的生态水位要求.生态保障度越高则湖泊生态系统越健康.
生态水位保障度的计算公式为:
| $ {\alpha _{ij}} = \frac{{{D_{ij}}}}{D} = \frac{{\sum {{\mathop{\rm sgn}} } \left( {{Z_{ijk}} - {Z_j}} \right)}}{D} $ | (2) |
式中,αij表示第i年第j月的生态水位保障度;Dij表示第i年第j月生态水位的保障天数;D表示第i年第j月的总天数.
其中:
| $ {\mathop{\rm sgn}} \left( {{Z_{ijk}} - {Z_j}} \right) = \left\{ {\begin{array}{*{20}{l}} 1&{{Z_{ijk}} > {Z_j}}\\ 0&{{Z_{ijk}} \le {Z_j}} \end{array}} \right. $ | (3) |
式中,Zijk表示第i年第j月第k日的湖泊日水位(m);Zj表示第i年第j月的生态水位(m).
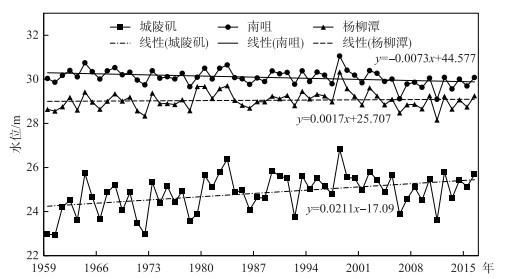
2 结果分析 2.1 洞庭湖年均水位趋势及其突变性分析如图 2所示,通过点绘1959—2016年年平均水位年际变化过程曲线可知,研究期间,洞庭湖水系年平均水位除1965、1972、1983、1992、1998、2006、2011年特枯年或特大洪水年的波动幅度较大外,城陵矶和杨柳潭呈增长趋势,南咀呈缓慢降低趋势.运用M-K检验法检验3个站点年平均水位变化的趋势性可知,城陵矶、杨柳潭年平均水位总体呈微弱上升态势,其中杨柳潭上升趋势未通过显著性检验,城陵矶上升趋势通过了95 %置信度检验;南咀年均水位呈下降态势,且下降趋势通过了95 %置信度检验.
|
图 2 洞庭湖年均水位变化 Fig.2 Annual water level changes of Lake Dongting |
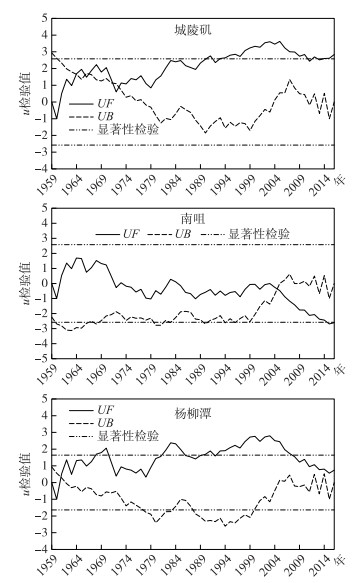
运用M-K检验法、累积距平法和滑动T检验法,对洞庭湖城陵矶、南咀、杨柳潭3个水文控制站研究期间的年均水位序列进行突变年份检验(图 3).通过以上3种检测方法综合判别洞庭湖3个水文站点理论上的突变年份(表 1).
|
图 3 Mann-Kendall突变性分析 Fig.3 Mutation analysis by Mann-Kendall |
| 表 1 洞庭湖3个水文站年均水位突变统计结果 Tab. 1 Statistical results of annual average water level of three hydrological stations in Lake Dongting |
为了便于研究,统一将2003年以前洞庭湖日水位过程作为自然基准水位序列,2003—2016年洞庭湖日水位过程作为水文变异后的水位改变序列.在此基础上运用生态水位年内展布法和RVA法对洞庭湖进行最小生态水位和适宜生态水位的计算.
2.2 洞庭湖生态水位计算最低生态水位为主要考虑防止湖泊生态系统进一步衰退的水位,保护湖泊核心区的水位,保护湿地水文要求以及保护水生生物的最低水位,在该水位要求下大部分湿地生态能够保存基本的生态活动,满足生态系统的基本运转,但是如果长时间处于该水位将会导致生物生长发展的缺失,最终导致生物的消亡.基于洞庭湖的湖泊实际情况,将湖泊生态需水划分为湖泊最小生态水位计算和湖泊适宜生态水位计算,通过洞庭湖突变发生前(1959—2002年)天然水位日均资料,运用生态水位年内展布法确定湖泊的最小生态水位.
湖泊适宜生态水位在最小生态水位的基础上强调了生态系统的完整性,在保护水生植物和水生动物的基础上,更进一步强调湖泊湿地生态系统中鸟类的保护,比最小生态水位有更高的要求.基于湖泊湿地生态系统中的水生植物及水生动物以及鸟类对水位的最低要求,采用基于IHA-RVA法的湖泊适宜生态水位计算方法,其原理是认为湖泊宜生态水位变动范围不应超过天然可变范围(即RVA阈值),这样才能够维持湖泊健康生态系统.
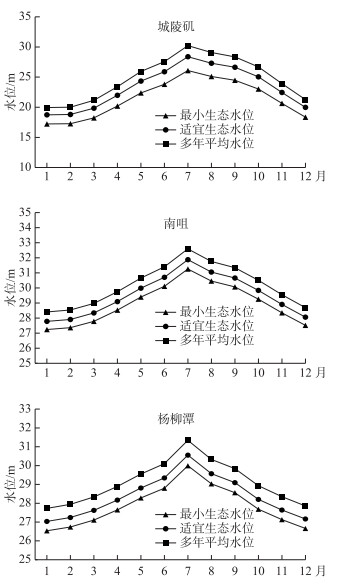
根据湖泊生态水位计算方法,选取洞庭湖水系城陵矶、南咀、杨柳潭3个水位站的典型水文站1959—2002年的近天然日水位资料,通过生态水位年内展布法计算湖泊生态水位,并以Tennant法进行验证,选取多年平均水位、最小年均水位和适宜年均水位,计算各水文站的同期均值比(表 2),并以多年月均水位过程为基准(表 3),计算各水文站基本生态水位和适宜生态水位年内水位过程,计算结果见表 4. 图 4为洞庭湖生态水位过程.
|
图 4 洞庭湖生态水位 Fig.4 Ecological water level in Lake Dongting |
| 表 2 洞庭湖各水文站的同期均值比 Tab. 2 The mean ratio of hydrologic stations in Lake Dongting in the same period |
| 表 3 洞庭湖各水文站的多年天然月均水位过程 Tab. 3 The process of natural monthly mean water level in each hydrological station of Lake Dongting |
| 表 4 洞庭湖各水文站的最小和适宜生态水位 Tab. 4 Minimum and suitable ecological water level of hydrological stations in Lake Dongting |
东洞庭湖、西洞庭湖和南洞庭湖的最低生态水位同期均值比分别为86.3 %、95.9 %和95.7 %,三者的适宜生态水位同期均值比依次为93.9 %、97.8 %和97.5 % (表 2).可以看出除东洞庭的最低生态水位同期均值比低于90 %,其余均高于90 %,可以推断出东洞庭湖的最小水位和平均水位间隔较大.东洞庭的年内水位波动最大,最高水位与最低水位相差10.26 m,而南洞庭和西洞庭则相差较小,分别为3.61和4.19 m.年内水位最高都发生在7月,最低水位都在1月(表 3).在空间分布上西洞庭湖的水位原本就比南洞庭和东洞庭湖的水位要高些,当地生物在历史演变过程中也慢慢适应了在该水位下生存,所以计算出来的适宜和最小生态水位相比较南洞庭和东洞庭湖水位都更高些(表 4).在动植物生长的旺盛期(5—10月)需要较高的水位来满足其繁殖需求,洞庭湖年内最高水位需求都出现在7月,东洞庭湖、南洞庭湖和西洞庭湖的适宜生态水位分别达到28.38、30.56 m和31.88 m.洞庭湖水位波动较大,长期高水位会引起敞水区面积增加,沉水植被向近岸区域扩展,深水区收缩,引起适宜高水位的外来物种的大量繁殖,降低物种多样性;水位上升还会增加对堤岸的侵蚀,降低底质中的溶解氧,增大磷的释放率,引起水体的富营养化.长期低水位会减少敞水区和湖滨带的面积,导致无脊椎动物和鱼类栖息地范围和大型植物的生物量减少,这就会造成生物多样性和生产力降低.因此,生态水位对保障洞庭湖生态系统的健康至关重要.
为了分析本研究成果合理性,采用Tennant法评价标准进行对比,在Tennant法评价中,以预先确定的多年平均流量百分数为基础,将保护水生态河水环境的河流流量推荐值分为最大允许极限值(200 %)、最佳范围值(60 % ~100 %)、极好状态值(枯水期40 %,丰水期60 %)、很好状态值(枯水期30 %,丰水期50 %)、良好状态值(枯水期20 %,丰水期40 %)、一般状态值((枯水期10 %,丰水期30 %))、差状态值(10 %)和极差状态值(0~10 %).其评价结果见表 5.
| 表 5 洞庭湖生态水位Tennant法评价 Tab. 5 Evaluation of the Tennant method for the ecological water level of Lake Dongting |
本文根据洞庭湖区水文特征,将Tennant法的丰水期修正为4—9月,枯水期修正为10月至翌年3月,根据计算结果与Tennant法比较可知,洞庭湖各水文断面的基本生态水位计算结果与修正后的Tennant法评价标准进行对比分析,在枯水期(10—3月)各个水文断面生态水位占多年年均水位的77.1 % ~94.4 %,根据Tennant法评价均处在最佳范围,此时湖泊水文条件仍要保持一定的水深、流速、河宽,满足生物生存、洄游、景观的一般要求,是绝大多数水生生物维持短时间生存的水位推荐值.在丰水期(4—9月),各水文断面生态水位占多年年均水位的95.5 % ~103.9 %,处于最佳范围,能够满足水生生物栖息和产卵、育幼等目标的水位需求.因此利用生态水位年内展布计算法计算的最小生态水位和IHA-RVA法计算出的适宜生态水位与Tennant法设定的分期相符,能够满足湖泊生态目标的需求.
关于洞庭湖生态水位的相关研究,谢永宏、梁婕和程俊翔等分别针对洞庭湖城陵矶水文站进行分析[9-11],计算出最小生态水位为25 m左右,与本研究计算分析的枯水期结果(19.1 m)相比明显偏大,另外这些研究只是计算出一个数值,而本研究计算的生态水位是一个水位过程.而杨毓鑫等采用多种方法计算洞庭湖最低生态水位[21],其中东洞庭湖、南洞庭湖和西洞庭湖分别为22.62、27.19和28.11 m,与本研究的结果相差不大.黄兵等认为湖泊适宜的生态水位为频率最大处月平均水位[22],通过计算得出东洞庭湖为24.39 m,南洞庭湖为25.61 m,西洞庭湖为30.2 m,而本研究计算得到东洞庭湖、南洞庭湖和西洞庭湖分别为23.29、28.36和29.51 m,计算结果基本一致,只有南洞庭湖差别较大,其原因是本研究选用了杨柳潭水文站,而黄兵等选用了鹿角水文站.总体而言,本研究相对前人研究结果更具有可操作性,其结果也更加符合湖泊天然水位变化规律.
2.3 洞庭湖水文突变前后保障程度根据前文得到的洞庭湖水文突变时间节点,将洞庭湖城陵矶、南咀、杨柳潭3个控制站点1959—2016年间的日平均水位数据分成水文突变前(1959—2002年)和突变后(2003—2016年),分别计算突变前、后3个水文站的最低生态水位和适宜生态水位保证率,计算结果见图 5.
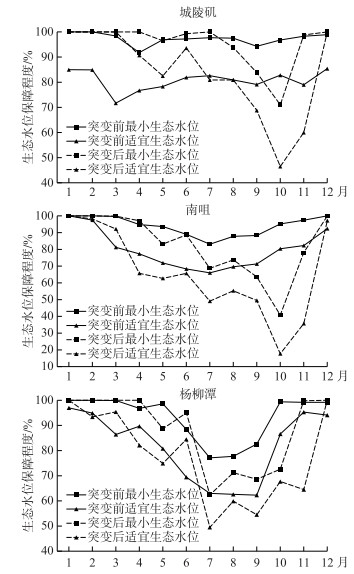
|
图 5 洞庭湖各站点突变前后生态水位保障程度 Fig.5 The guarantee degree of ecological water level before and after the abrupt change in Lake Dongting |
根据图 5可知,水文突变前(1959—2002年)洞庭湖城陵矶、南咀、杨柳潭水文站的最小生态水位保障程度普遍较高.其中,以城陵矶站最小生态水位保障程度最高,年内共有6个月的日均保障程度达到100 %,年保障程度也达到94.4 %;而南咀相对较低,年保障程度为82.7 %,尤其在7、8、9、10月的保障程度不足80 %.通过适宜生态水位的保障程度分析可知,城陵矶站依然保持着较高的保障程度,达到84.2 %;杨柳潭的适宜生态水位保障程度虽然有一定的下降,但还保持良好,仍在75 %以上;南咀站的适宜生态水位保障程度有些偏低,8—11月的保障程度都在50 %以下.从年内各月份保障程度的对比看,洞庭湖各站点适宜生态水位保障程度与最小生态水位保障程度相似,均在8、9、10月的保障程度较低.水文突变后(2003—2016年)城陵矶、南咀、杨柳潭水文站的最小和适宜生态水位保障程度相对于水文突变前普遍偏低,尤其是汛期,其中8、9、10月生态水位保障程度下降明显.从总体上来看,枯水期(11—4月)的保障程度都较高,在汛期(8—10月)生态水位保障程度偏低,说明长江中上游的梯级水库在枯水期的调度作用明显.汛期生态水文保障程度偏低应该引起重视,在满足湖泊防洪工程的基础上,尽量保持该时期湖泊内的水位,以维持湖泊生态系统健康.
3 结论本文将洞庭湖区域城陵矶、杨柳潭、南咀3个水文站1959—2016年实测日均水位运用M-K突变分析法结合累积距平法、滑动T检验法找出长时间轴上的突变点,认为在1959—2002年是洞庭湖区域在自然发展状态下,对该时间序列的日均水位进行分析,利用年内展布法和结合IHA-RVA法的适宜生态水位计算法得出3个站点的最小生态水位和适宜生态水位,并以Tenntant法进行验证,进而对最小生态水位和适宜生态水位在水文突变前后的保障度进行研究,得出以下结论:
1) 洞庭湖城陵矶和杨柳潭水文站年均水位呈上升趋势,而且城陵矶站水位上升趋势显著,南咀站年均水位呈显著下降趋势.洞庭湖水位年际变化突变年份为2003年,突变年份基本上与三峡工程蓄水时间相符,选取1959—2002年为近天然状况下水位序列,2003—2013年为水文突变后水位序列.
2) 根据水文突变前水位序列计算出城陵矶、南咀和杨柳潭年均最小生态水位分别为21.41、28.95和27.84 m,分别占多年平均水位的86.3 %、95.9 %和95.7 %;城陵矶、南咀和杨柳潭年均适宜生态水位分别为23.29、29.51和28.36 m,分别占多年平均水位的93.9 %、97.8 %和97.5 %;洞庭湖年内生态水位差别较大,其中1月份水位最低,7月份水位最高;参考Tennant法评价标准可知,利用生态水位年内展布法和IHA-RVA法计算出的最小和适宜生态水位都与Tennant法设定的分期相符,能够满足河流生态目标的需求,计算结果较为合理.
3) 根据生态水位保障度计算分析,城陵矶水文站的水文突变后生态水位保障度相对较高,除10月份保障程度下降,其他月份的保障程度均高于突变以前的保障程度;南咀站和杨柳潭站水文突变后的保障程度相对较差,大部分月份的保障程度都比突变前的保障程度低.从总体来看,枯水期(11—4月)的保障程度较高,在汛期(8—10月)生态水位保障程度偏低,尤其是10月,最小和生态水位保障度大幅度下降,这与该时段洞庭湖流域上游水库蓄水导致洞庭湖水位下降有直接关系.
4) 针对洞庭湖生态水位保障问题,特别是生态水位在10月各站点均出现保障程度大幅下降的情况,适当在该期间补充水量,延迟湖泊洼地水位提前下降对湿地提前出露的影响,为水生植物和水生动物提供较稳定的环境,保障湖区生态安全.
| [1] |
Yang GS ed. Yangtze conservation and development report 2011. Wuhan: Yangtze Press, 2011. [杨桂山. 长江保护与发展报告2011. 武汉: 长江出版社, 2011.]
|
| [2] |
Xie YH, Wang KL, Ren B et al. Evolution, problems and protection measures of ecological environments in Dongting Lake area. Research of Agricultural Modernization, 2007, 28(6): 677-681. [谢永宏, 王克林, 任勃等. 洞庭湖生态环境的演变、问题及保护措施. 农业现代化研究, 2007, 28(6): 677-681.] |
| [3] |
Zacharias I, Dimitriou E, Koussouris T. Integrated water management scenarios for wetland protection:application in Trichonis Lake. Environmental Modelling & Software, 2005, 20(2): 177-185. |
| [4] |
Desgranges JL, Ingram J, Drolet B et al. Modelling wetland bird response to water level changes in the Lake Ontario-St. Lawrence River hydrosystem. Environmental Monitoring and Assessment, 2006, 113(1/3): 329-365. |
| [5] |
Hudon C, Wilcox D, Ingram J. Modeling wetland plant community response to assess water-level regulation scenarios in the lake Ontario-st. Lawrence river basin. Environmental Monitoring and Assessment, 2006, 113(1/2/3): 303-328. DOI:10.1007/s10661-005-9086-4 |
| [6] |
Cui BS, Zhao X, Yang ZF. Eco-hydrology-based calculation of the minimum ecological water requirement for lakes. Acta Ecologica Sinica, 2005, 25(7): 1788-1795. [崔保山, 赵翔, 杨志峰. 基于生态水文学原理的湖泊最小生态需水量计算. 生态学报, 2005, 25(7): 1788-1795.] |
| [7] |
Li XH, Song YD, Zahng FD et al. The calculation of the lowest ecological water level of Lake Bosten. J Lake Sci, 2007, 19(2): 177-181. [李新虎, 宋郁东, 张奋东等. 博斯腾湖最低生态水位计算. 湖泊科学, 2007, 19(2): 177-181. DOI:10.18307/2007.0211] |
| [8] |
Gan F, Tang L, Guo HC et al. New method and application of estimating ecological water level of the Lake Poyang. J Lake Sci, 2015, 27(5): 783-790. [淦峰, 唐琳, 郭怀成等. 湖泊生态水位计算新方法与应用. 湖泊科学, 2015, 27(5): 783-790. DOI:10.18307/2015.0504] |
| [9] |
Xie YH, Li F, Chen XS. Study on the minimum ecological water demand for the Dongting Lake. Resources and Environment in the Yangtze Basin, 2012, 21(1): 64-70. [谢永宏, 李峰, 陈心胜. 洞庭湖最小生态需水量研究. 长江流域资源与环境, 2012, 21(1): 64-70.] |
| [10] |
Liang J, Peng YR, Guo SL et al. Determination of ecological water-level in the eastern Lake Dongting with hydrological alterations. J Lake Sci, 2013, 25(3): 330-334. [梁婕, 彭也茹, 郭生练等. 基于水文变异的东洞庭湖湿地生态水位研究. 湖泊科学, 2013, 25(3): 330-334. DOI:10.18307/2013.0303] |
| [11] |
Ceng JX, Xu LG, Wu R et al. Study on the lowest ecological water level of east Dongting Lake. Jiangxi Science, 2015(6): 932-937. [程俊翔, 徐力刚, 吴睿等. 东洞庭湖最低生态水位研究. 江西科学, 2015(6): 932-937.] |
| [12] |
Pan ZR, Ruan XH, Xu J. A new calculation method of instream basic ecological water demand. Journal of Hydraulic Engineering, 2013, 44(1): 119-126. [潘扎荣, 阮晓红, 徐静. 河道基本生态需水的年内展布计算法. 水利学报, 2013, 44(1): 119-126.] |
| [13] |
Richter B, Baumgartner J, Wigington R et al. How much water does a river need?. Freshwater Biology, 1997, 37(1): 231-249. DOI:10.1046/j.1365-2427.1997.00153.x |
| [14] |
Zhang DW, Cong ZT, Ni GH. Comparison of three Mann-Kendall methods based on the China's meteorological data. Advances in Water Science, 2013, 24(4): 490-496. [章诞武, 丛振涛, 倪广恒. 基于中国气象资料的趋势检验方法对比分析. 水科学进展, 2013, 24(4): 490-496.] |
| [15] |
Li JB, Luo ZH, Ye YY et al. Eco-hydrological impacts of Three Gorges Reservoir's operation on three outfalls of Chingjiang River. Chinese Journal of Applied Ecology, 2016, 27(4): 1285-1293. [李景保, 罗中海, 叶亚亚等. 三峡水库运行对长江荆南三口水文和生态的影响. 应用生态学报, 2016, 27(4): 1285-1293. DOI:10.13287/j.1001-9332.201604.023] |
| [16] |
Lu LL, Li ZX. Variability recognition of runoff in the middle and lower reaches of Yarlung Zangbo River. Water Power, 2013, 39(5): 12-15. [吕琳莉, 李朝霞. 雅鲁藏布江中下游径流变异性识别. 水力发电, 2013, 39(5): 12-15.] |
| [17] |
Liang Y. The research of instream environmental water requirement in Huaihe river system[Dissertation]. Beijing: Tsinghua Univesity, 2008. [梁友.淮河水系河湖生态需水量研究[学位论文].北京: 清华大学, 2008. ]
|
| [18] |
Richter BD, Baumgartner JV, Powell J et al. A method for assessing hydrologic alteration within ecosystems. Conservation Biology, 1996, 10(4): 1163-1174. DOI:10.1046/j.1523-1739.1996.10041163.x |
| [19] |
Mathews R, Richter BD. Application of the indicators of hydrologic alteration software in environmental flow Setting1. JAWRA Journal of the American Water Resources Association, 2007, 43(6): 1400-1413. DOI:10.1111/j.1752-1688.2007.00099.x |
| [20] |
Pan ZR, Ruan XH. Spatio-temporal analysis of satisfactory degree of ecological water demand in Huaihe River Basin. Journal of Hydraulic Engineering, 2015, 46(3): 280-290. [潘扎荣, 阮晓红. 淮河流域河道内生态需水保障程度时空特征解析. 水利学报, 2015, 46(3): 280-290.] |
| [21] |
Yang YX, Du CY, Zhang JF et al. Determination of lowest ecological water level in Dongting Lake area. Water Resources Protection, 2019, 35(3): 89-94. [杨毓鑫, 杜春艳, 张金帆等. 洞庭湖湖区最低生态水位的确定. 水资源保护, 2019, 35(3): 89-94.] |
| [22] |
Huang B, Jiang H, Liao XH et al. Evaluation of ecological water-level in the Dongting Lake with hydrological alterations. China Rural Water and Hydropower, 2019(3): 88-96. [黄兵, 姜恒, 廖小红等. 水文变异条件下的洞庭湖生态水位研究. 中国农村水利水电, 2019(3): 88-96.] |
 2020, Vol. 32
2020, Vol. 32 

