(2: 水利部水文局, 北京 100053)
(3: 黄河水文水资源科学研究院, 郑州 450004)
(2: Bureau of Hydrology, Ministry of Water Resources of China, Beijing 100053, P. R. China)
(3: Yellow River Institute of Hydrology and Water Resources, Zhengzhou 450004, P. R. China)
中国北方半干旱地区的降水与下垫面条件具有明显的时空异质性,下垫面条件复杂,地表植被覆盖较差,降水对土层的入渗能力弱且作用层浅,表层土壤含水量变化剧烈[1]. 因此,北方半干旱地区的产流过程中极易出现蓄满产流和超渗产流交替主导的现象[2-3]. 此外,该类地区的降水历时短、强度大、汇流速度极快,极易产生陡涨陡落的洪水[4-6],从而造成了严重的生命和财产损失. 水文预报模型作为最为重要和基础的非工程性防洪减灾措施之一,目前其在半干旱地区的研制和应用主要存在以下两类问题:数据精度的满足性和模型结构的合理性[6].
针对半干旱地区水文资料短缺情况,早期学者们着力研究降雨时空处理技术[7],如空间处理有反距离平均法、克里金法、泰森多边形等,降雨时间处理有线性插值法、分形相似理论等[8-9],以期可以通过实现降雨分辨率的时空分布来解决资料短缺或精度不足问题,但事实证明,这些技术受限于观测数据本身的精度[10]. 随着遥感观测技术的进步和基于卫星数据反演算法的改进,卫星降水数据逐渐成为水文研究中的重要数据来源[11]. 但卫星降水数据与地面雨量站观测数据融合的精度是否达到半干旱地区中小流域的洪水预报要求,这些研究是有限的. 因此,对于半干旱的中小流域而言,利用卫星数据弥补数据精度及资料种类的研究还不够成熟,在防洪实践中仍依赖于地面雨量站的观测数据.
另一方面,学者们为了寻找适应于半干旱地区水文模型的稳定结构,做了大量的野外试验和数值模拟,研制出了多种类型的水文模型[12],从单一产流模型到混合产流模型如垂向混合径流模型[13]、增加超渗的新安江模型[2]、新安江—海河模型[14]等,再到目前较为流行的灵活框架模型如FUSE[15]、FARM[16]及SCCM[17]等,取得了阶段性的研究成果. 但不可否认的是,目前半干旱地区的洪水模拟精度相比湿润半湿润地区仍然差强人意.
近些年来,随着半干旱地区洪水预报研究的不断深入,许多学者还发现了水文模型结构、参数优化率定、降水数据精度等因素之间还存在着互馈的关系. 基于此国内外学者对不同气候条件,不同时空尺度下的水文模型参数优选及径流模拟开展了大量的研究[18-20]. Ostrowski和Wolft[21]发现确定性水文模型参数与所选的模型时间步长高度相关. Krajewski等[22]发现了水文响应对时间尺度的敏感度要高于对空间尺度的敏感度. 王盛萍等[23]发现时间步长的变化对洪峰过程的模拟具有显著的影响. 夏军等[24]在无定河流域的研究指出该地区的水文模拟结果很大程度上取决于资料的精度. 这些研究多以时间或空间、或时空组合对洪水响应的影响,尚未形成系统的理论体系和成熟的方法技术,这对产流机制的复杂性叠加降雨时空的差异性的半干旱地区洪水预报作业需求是远远不够的.
本文基于将水文实验和水文模拟技术有机地结合的思想,选择典型中国半干旱地区的实验场区,基于流域的原始观测数据,采用降雨相似分形方法和距离平方倒数方法分别从时间和空间维度进行插值处理,得到不同时空尺度的降雨方案,将设定好具有变化规律性的降水方案作为输入加载至三种不同产流机制的水文模型(蓄满模型、超渗模型、混合模型)中进行洪水模拟,分别得到若干个“时—空—模”模拟方案结果,通过对比分析不同方案的计算结果去探究时间、空间、产流机制等因素对半干旱地区洪水模拟的影响,以期能够系统地揭示半干旱地区降雨径流模拟的困难,为该类地区水文模型的研制工作提供借鉴.
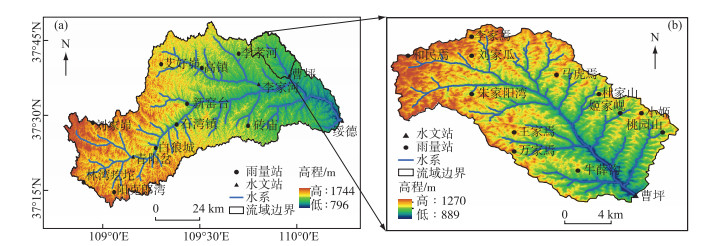
1 研究流域和数据 1.1 研究区概况本文选择了中国北方半干旱地区的实验流域——大理河绥德站和曹坪站以上流域作为研究区(以下简称绥德流域和曹坪流域). 绥德流域(图 1a; 37°30′~37°56′N, 109°14′~110°13′E)流域面积为3893 km2;曹坪流域(图 1b)位于绥德流域的下游,流域面积为187 km2,是嵌套在绥德流域下游的小流域(图 1). 大理河流域属于典型大陆性季风气候区,流域多年平均气温7.8~9.6℃. 降雨量的年内分配不均,主要集中在6—9月,雨量占比可达全年的60 % ~70 %,大理河的洪水主要是由暴雨形成,洪水的大小主要取决于暴雨面积和强度. 暴雨发生时多数为局地暴雨,其范围小、历时短、强度大,易造成山洪暴发,流域内的地貌主要为黄土丘陵沟谷,气候干旱,植被覆盖率较低,土壤侵蚀非常严重.
|
图 1 绥德流域(a)和曹坪流域(b)的位置、高程、水系及站点分布 Fig.1 Location, elevation, rivers and stations distribution of the Suide(a) and Caoping(b) Watersheds |
本研究所需下垫面数据为数字高程地图(DEM)、土壤类型和土地利用类型数据. DEM从地理空间数据云网站下载,选择GDEMV2 DEM数字高程数据产品,分辨率为30 m. 土壤数据来源于联合国粮农组织(FAO),1 ∶100万土壤栅格数据资料. 土地利用数据是从国家基础地理信息中心下载的GlobeLand30产品,分辨率为30 m的栅格文件.
绥德流域和曹坪流域所需的水文气象资料包括降水量、蒸发量和断面流量,分别由陕西水文局和黄河水利委员会水文局提供. 绥德流域有4个水文站,10个雨量站,站点密度约为278 km2/站(图 1a);曹坪流域有1个水文站,12个雨量站,站点密度较高,约为14 km2/站(图 1b),所有的水文站均包含降雨观测数据. 两个流域的蒸发量数据均来自绥德站同期观测的水面蒸发数据. 在原始的降雨观测资料中,绥德流域雨量记录间隔为1~2 h;曹坪流域的实测降雨资料时间分辨率大约为5~20 min,实测径流资料的时间分辨率大约为5~10 min. 由于绥德流域和曹坪流域数据来源不同,加上观测数据不同期,在构建降雨方案时,曹坪流域的雨量站不包含在绥德流域内.
选取绥德流域2010—2018年的19场洪水事件和曹坪流域2000—2010年的17场洪水事件进行模型模拟. 两个实验流域所选取的洪水中均包含低峰洪水、中峰洪水、高峰洪水,以使输入模型的资料能充分地对模型进行系统参数优化.
2 研究方法 2.1 基于时空尺度分析构建降雨方案 2.1.1 降雨方案的时间尺度处理本研究采用分形理论的自相似性(既小时间尺度上降雨的分布规律与大时间尺度上降雨分布规律相似)对降雨资料进行解集或聚集,将原始降雨资料处理成指定间隔的降雨资料,最终形成M个不同时间步长的数据集. 具体计算方法通过此例来介绍:在t时段的原始降雨为Pt0,t+1时段的原始降雨为Pt+10,根据当前时段与上时段降雨的关系,计算得到t+1时段的新降雨量为P′t+1,原始的t+1时段的降雨量Pt+10扣除新降雨量P′t+1,剩余部分则为t+0.5时段的降雨量为P′t+0.5,计算数学表达式为:
| $ \begin{aligned} &P_{t+1}^{\prime}=\frac{P_{t+1}^{0}{ }^{2}}{\left(P_{t}^{0}+P_{t+1}^{0}\right)} \end{aligned} $ | (1) |
| $ \begin{aligned} &P_{t+0.5}^{\prime}=P_{t+1}^{0}-P_{t+1}^{\prime} \end{aligned} $ | (2) |
借鉴抽站法的概念,采取两个策略进行抽取:1)从密集站点区域抽取;2)上下游对称抽取,从流域中所有雨量站中均匀地抽取部分雨量站,得到N种不同密度的雨量站空间分布方案,并采用距离平方倒数法,对每种方案的雨量数据进行空间插值. 第i个网格的降水量Pi的计算数学表达式为:
| $ \begin{gathered} P_{i}=\sum\limits_{j=1}^{k} w_{i, j} \cdot P_{j} \end{gathered} $ | (3) |
| $ \begin{gathered} w_{i, j}=\frac{d_{i, j}{ }^{2}}{\sum\limits_{z=1}^{b} d_{z}{ }^{2}} \end{gathered} $ | (4) |
式中,Pj为第j个雨量站的降雨量,wi, j为第i个网格相对于第j个雨量站的权重系数,di, j为第i个网格相对于第j个雨量站的距离,b为每种方案中雨量站个数,k为距第i个网格最近的k个雨量站.
通过以上方法,对原始的观测数据进行时间步长和空间雨量站密度的处理,最终得到M*N种不同时空分布的降雨方案.
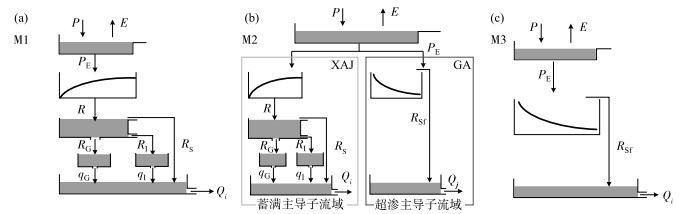
2.2 多产流机制的水文模型构建在半干旱地区,由于下垫面和降水时空分布不均匀,超渗产流和蓄满产流随时空变化的现象尤为明显,伴随产生的径流被称为混合产流[13, 25]. 在本研究中,采用3种产流机制的水文模型,分别为:代表蓄满产流的新安江模型、代表超渗产流的Green-Ampt模型和基于两者之间的蓄超组合模型(新安江与Green-Ampt的组合模型). 3个模型按照产流机制从蓄满产流逐渐过渡到超渗产流分别为:新安江模型、蓄超组合模型、Green-Ampt模型. 为方便方法的描述和结果的展示,将3个模型分别称为:M1、M2和M3. 各个模型的物理结构如图 2所示.
|
图 2 M1、M2和M3概念水文模型的示意图(P降雨量,E蒸发量,PE净雨量,R蓄满产流量,RG地下径流量,RI壤中径流量,RS地表径流量,RSf超渗地表径流,qG地下坡面汇流,qI壤中坡面汇流量,Qi子流域出流量) Fig.2 Schematic representation of the conceptual hydrological models M1, M2 and M3 |
新安江模型[26](M1模型)是一个经典的概念性水文模型,核心是基于抛物线概率分布的降雨—径流本构关系,先产流,后分水源,是典型的蓄满产流模型. 新安江模型由蒸散发、产流、分水源和汇流4个模块,17个参数组成. 其原理简单明确,计算效率高,被广泛应用于中国湿润地区的洪水预报.
2.2.2 超渗模型Green-Ampt模型[27](M3模型)是由GREEN和AMPT等于1911年提出的一种积水条件下均质土壤下渗模型,是典型的超渗产流模型. Green-Ampt模型由蒸散发、产流和汇流三个模块组成. 模型通过Green-Ampt下渗公式与下渗能力分布曲线组合计算超渗地表径流,不考虑壤中流和地下径流. 模型具有表达式简单、参数较少和物理意义明确等特点,被广泛应用于中国干旱地区的洪水预报.
2.2.3 蓄超组合模型基于主导性水文过程的概念,划分蓄满产流子流域与超渗产流子流域,通过新安江模型和Green-Ampt模型构建蓄超组合模型[28](M2模型). 具体操作步骤如下:(1)采用CN-TI指数法,将研究区划分为超渗主导子流域和蓄满主导子流域,详细方法介绍参见文献[1]. (2)基于子流域蓄超划分结果构建蓄超空间组合模型. 即在新安江模型的产流模块中引入Green-Ampt下渗曲线,与原有张力水蓄水容量曲线组成两种产流计算方法. 在产流计算时,蓄满主导子流域使用张力水蓄水容量曲线计算,超渗主导子流域使用下渗容量曲线. 该模型可实现蓄满超渗子流域的快速划分,进而灵活调整产流计算模型,以适应半湿润半干旱区域复杂的地形地貌[1, 28].
2.2.4 模型参数率定将不同时空分布的降雨方案作为输入加载至3种模型中进行模拟,并分别完成每种降雨方案的最优参数率定. 为了减少率定过程中参数的不确定性,减轻计算工作量,本文仅对敏感参数使用SCE-UA算法[29]自动优化,不敏感参数由人工试错法估计. 其中,M1模型的敏感参数为自由水容量SM、地表水消退系数CS;M3模型的敏感参数为饱和导水率KS、湿润锋出土吸力Sf;由于M2模型包含了前两个模型的产流模式,所以其敏感参数也保持一致. 在每个流域中选择了3场洪水事件来验证校准后的模型,为了方便分析,将参与率定和检验的所有场次洪水的模拟结果整合在一起统计综合模拟效果.
2.3 多层次评价分析 2.3.1 降雨方案异质性评价采用两个降雨变化的特征参数分析降雨方案的差异,流域累计面平均雨量和表示降雨空间离散程度的变差系数(Cv),计算方程为:
| $ \begin{gathered} \bar{P}=\sum\limits_{i=1}^{m} \alpha_{i} P_{i} \end{gathered} $ | (5) |
| $ \begin{gathered} C_{\mathrm{v}}=\frac{\sqrt{\sum\limits_{i=1}^{m} \alpha_{i}\left(P_{i}-\bar{P}\right)^{2}}}{\bar{P}} \end{gathered} $ | (6) |
式中,αi为第i 个网格的权重指数;Pi为第i个网格的累计降雨量;m为网格单元的个数.
2.3.2 模型结果评价依据传统的水文模拟与预报精度评定准则,结合半干旱地区洪水特征,参考《水文情报预报规范》[30]规定,选择4种评价指标:径流深相对误差合格率(NR),该误差以实测值的20 % 作为许可误差,当该值大于20 mm时取20 mm,当小于3 mm时取3 mm;洪峰相对误差合格率(NQ),以实测洪峰的20 % 作为许可误差判定预报洪峰是否合格;峰现时差合格率(NT),以峰现时间小于3 h为许可误差;平均纳什系数(NS),评价洪水实测过程与预报过程之间的拟合程度.
上述4个统计指标的取值范围不一致,需要进行归一化处理. 其中,采用MIN-MAX归一化方法,将NR、NQ、NT归一化到(0, 1),NS归一化到(-1, 1). 将归一化后的统计指标等权重累加求和,得到综合指标CI. 综合指标CI值越大,表明模拟精度越高. 每个方案的综合指标CIj计算如下:
| $ C I_{j}=N R_{j}^{\prime}+N Q_{j}^{\prime}+N T_{j}^{\prime}+N S_{j}^{\prime} $ | (7) |
式中,NR′j、NQ′j、NT′j、NS′j分别为第j个方案归一化后的NR、NQ、NT、NS.
3 结果分析与讨论 3.1 降雨方案结果分析研究流域位于半干旱地区,该类地区汛期降水具有短历时、强度大的特点,因此研究流域的时间步长和雨量站数量的设置均需在满足代表性的基础上体现差异性.
在时间步长方面,综合考虑研究流域的洪水历时、洪水起涨历时以及汇流历时,设置4种时间步长的方案(绥德流域15、30、60、120 min;曹坪流域5、10、20、30 min). 在雨量站数量方面,考虑到降雨数据的代表性,设置最少雨量站数量为总雨量站的一半. 本文采用抽站法,均匀地从研究流域所有雨量站中抽取不同数量的雨量站,分别得到5种不同雨量站的空间分布(绥德流域14、12、10、8、6;曹坪流域13、11、9、7、5). 最终,通过组合不同的时间步长和雨量站数量后,可以得到20种不同时空分布的降雨方案.
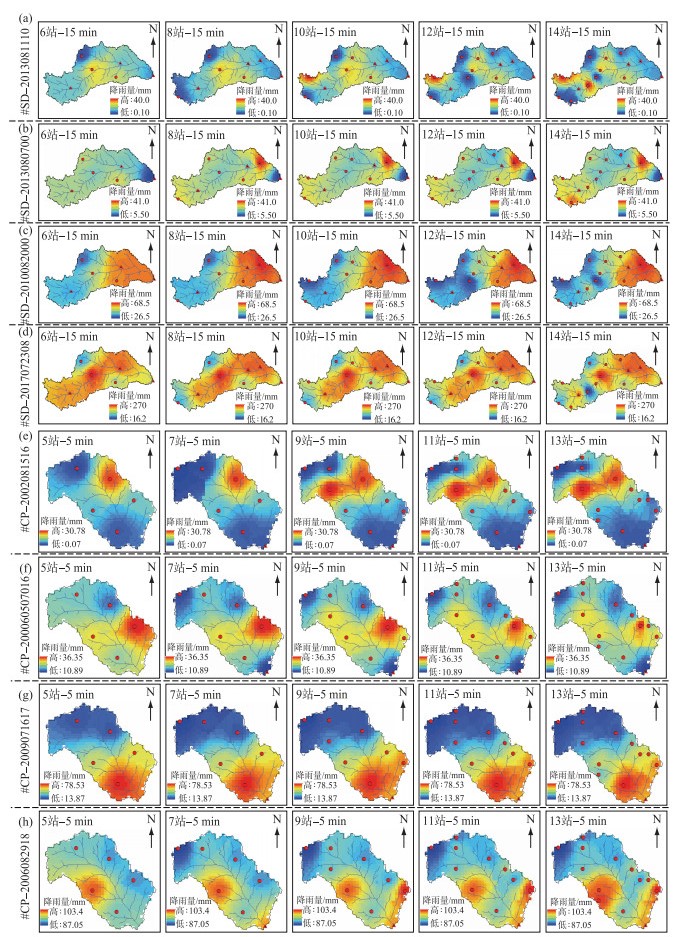
3.1.1 降雨方案时空分布结果由于降雨场次数量较多,降雨空间分布结果不便全部展示,因此,将流域面平均降雨量进行排序,选取四分位场次洪水:25 %、50 %、75 % 和降雨量最大场次(100 %)的4场次典型洪水进行展示. 图 3是两个研究流域4场次典型洪水的降雨空间方案分布图.
|
图 3 绥德流域(a~d)和曹坪流域(e~h)典型场次洪水降雨空间方案分布 Fig.3 The temporal distribution of rainfall of typical flood events in Suide (a-d) and Caoping (e-h) Watersheds |
对于绥德流域,随着测站数量的增加,4个洪水事件的降雨量分布特点如下. #SD-2013081110和#SD-2013080700的暴雨中心数量均发生了明显变化;但从降雨量分布来看,前者相对于后者变得越来越不均匀(图 3a和3b). #SD-2010082000和#SD-2017072308的暴雨中心没有明显变化,但上游雨量分布逐渐不均匀(图 3c和3d)). 在曹坪流域,随着雨量站数量的增加,#CP-2002081516的暴雨中心由1个变为2个(图 3e);#CP-2006050716的暴雨中心消失了,降雨量空间分布越来越均匀(图 3f);#CP-2009071617的暴雨中心范围有所缩小,降雨空间分布没有发生明显变化(图 3g);#CP-2006082918的暴雨中心数量增加且越来越明显(图 3h).
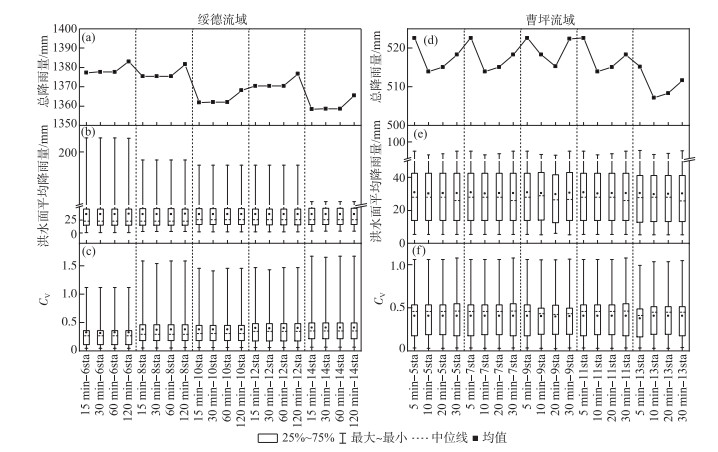
3.1.2 降雨方案的差异性评价本小节分析研究流域的20种时空降雨方案的差异性:图 4为绥德流域和曹坪流域的20种时空方案的全部洪水事件的降雨量差异性结果. 其中,图 4b和4e的“洪水面平均降雨量”是每场洪水的面平均降雨量,图 4a和4d的“总降雨量”是所有场次洪水的面平均降雨量总和. 可以看出,在绥德流域,随着雨量站数量的增加,降雨总量呈现减少趋势(图 4a,减少幅度约为20 mm),洪水事件的面降雨量的分布范围逐渐缩小(图 4b),降雨空间变异性逐渐增大(图 4c). 当雨量站数量一致时,随着时间步长的增加,两个流域的降雨总量呈现增加趋势,而洪水事件降雨量的分布范围和降雨空间的变异性没有明显变化趋势. 在曹坪流域,随着雨量站数量的增加,降雨总量呈现减少趋势(图 4d,减少幅度约为8 mm). 当雨量站数量一致时,随着时间步长的增加,降雨总量呈现陡减缓增的趋势,区间内变幅为10 mm左右. 而洪水事件降雨量的分布范围和降雨空间的变异性没有明显变化趋势(图 4d~f).
|
图 4 绥德流域(a~c)和曹坪流域(d~f)的4个典型洪水事件的20种时空方案的降雨量和空间变异性 Fig.4 20 spatiotemporal schemes (rainfall and spatial variability) for four typical flood events in Suide(a-c) and Caoping(d-f) Watersheds |
理论上,流域内的雨量站数量设置越多,对实测降雨的测量越精准. 但是通过上述结果可知,对于流域内发生的大多数的场次降雨来说,尽管对降雨的空间分布影响明显,但对降雨总量来说差别不大;另外,对于在量级大降雨的降雨总量变化稍微明显,但是这个微小变化基本是可以忽略的(占比较小).
通过上述结果可以大概看出,如果只是单独看降雨的差异性,不同时间步长和雨量站数量组合的降雨方案存在的差异性并不显著. 但是在半干旱地区,降雨强度对于产流计算起到十分关键的作用. 因此,下面重点从模型模拟方面,探讨不同时空组合的降雨方案对模型模拟结果的影响程度.
3.2 多模型模拟结果分析 3.2.1 “时—空—模”单因素评价指标结果将20种时空分布的降雨结果加载至3种水文模型中进行优化率定,得到60个“时—空—模”模拟方案的最优模拟结果. 在半干旱地区,洪水洪量小但洪峰高,形状陡涨陡落,需要更加关注洪峰模拟效果[12-14]. 因此,单因素评价中将径流深合格率、洪峰合格率与峰现时差合格率作为主要的评价指标,平均纳什效率系数作为参考指标.
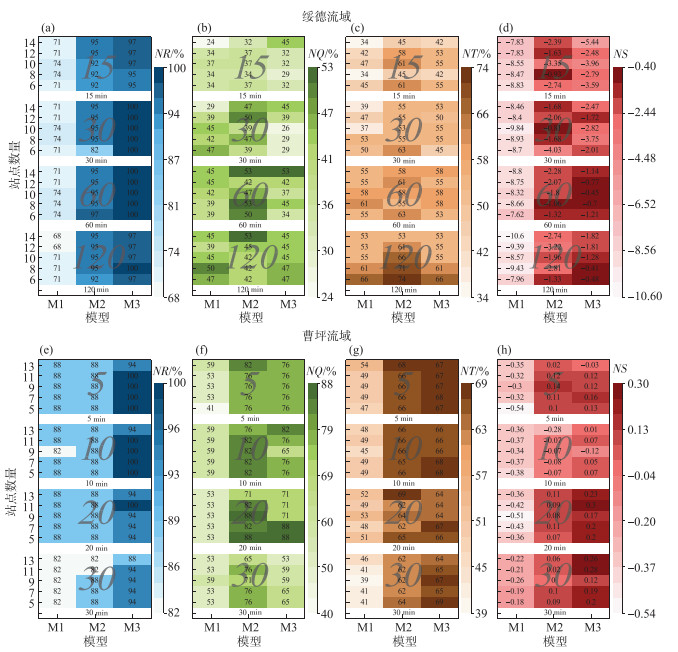
图 5为4个评价指标在2个研究流域的结果分布图,分别按照时间步长、空间雨量站数量及模型种类3个因素绘制流域模拟结果的4种评价指标的棋盘图. 每个棋盘图由若干个色块组成,例如,在图 5a的棋盘图中,按照时间步长将60种方案分为4组,每一组称为一个色块,每个色块内包含该时间步长对应的全部方案的评价指标计算结果. 棋盘图中,蓝色代表径流深合格率(NR),绿色为洪峰合格率(NQ),棕色为峰现时差合格率(NT),红色为平均纳什效率系数(NS). 颜色越深取值越大,代表模拟精度越高;反之,代表模拟精度低.
|
图 5 绥德流域(a~d)和曹坪流域(e~h)洪水模拟的单指标评价结果 Fig.5 The four evaluation indexes of simulation results in Suide(a-d) and Caoping(e-h) Watersheds |
(1) 按照时间差异性分组评价
在绥德流域,NR和NS对时间步长变化的响应不敏感(图 5a,d). 随着时间步长的增加,NQ呈现递增的趋势,在时间步长为60 min的色块中,整体取值较高;在15 min的色块中,NQ整体取值较低(图 5b);NT随时间步长的增加越来越高,最大值出现在120 min的色块中(图 5c). 在曹坪流域,随着时间步长的增加,NR和NT呈现略微降低的趋势(图 5e,g),而NS则出现增加的趋势(图 5h);NQ呈现先增后减的趋势,较大值聚集在时间步长为20 min的色块中,而时间步长为30 min的色块整体值偏低(图 5f).
绥德流域和曹坪流域属于半干旱流域,产流受降雨强度影响大. 从理论上讲,时间步长越小,降雨方案精度越高,模型对于洪水过程刻画越精细,模拟效果越接近真实值. 但从上述结果发现,模拟结果并都不是在最小时间步长时最好,尤其是绥德流域,4个评价指标里有3个是在60 min时最好,1个在120 min最好.
(2) 按照空间差异性分组评价
在绥德流域,随着雨量站数量的增加,NR在雨量站数量为12和14时,模拟结果基本相同(图 5a);NQ整体呈现先减后增的趋势(图 5b),在雨量站数量为14,整体值最大;NT递减的趋势显著(图 5c);NS则略微递减(图 5d). 在曹坪流域,NR和NT与雨量站数量之间的响应关系不敏感(图 5e,g);NQ随着雨量站数量的增加,整体呈现略微降低的趋势(图 5f);而NS整体呈现递增的趋势(图 5h).
从上述结果可以看出,研究区模拟结果并没有出现“雨量站数量越多,评价指标的值越高”的趋势性结果. 不论雨量站密度如何,4种评价指标都可以实现“较好的”模拟效果. 结合流域的典型降雨空间分布图(图 3)以及降雨量空间差异性结果(图 4)来看,流域中雨量站数量的减少,对于洪水事件的降雨的影响主要是暴雨中心的缺失以及面平均降雨量的微小差别. 虽然雨量站数量减少了,可以通过空间插值的方法进行插补并将降雨总雨量把控在小误差范围内,但插补后的降雨方案肯定不如有真实雨量站时对降雨空间分布刻画的精细. 对于小范围误差的降雨,研究发现,使用SCE-UA方法进行优化参数率定,总是可以通过对敏感参数的微小调整后对误差进行“抵消”,进而找到相似的洪水模拟结果. 然而,通过模型参数抵消输入数据的误差是水文模拟领域在构建模型和评价模型性能时极力避免的错误之一. 最主要的风险是,抵消误差不能真实反映降水输入数据的误差,可能导致模型的校准错误,对提高模拟能力起到反作用.
(3) 按照模型差异性分组评价
在绥德流域,随着模型序号的增加,NR呈现显著的增加趋势,合格率为100 % 的值全部聚集在M3模型中(图 5a);NQ随着模型序号的增加整体呈现先增后减的趋势,在M2模型整体取值较高(图 5b);NT整体分布相对较为均匀(图 5c);NS在M2和M3模型整体都较高且比较均匀(图 5d). 在曹坪流域,NR在M3模型的整体取值明显大于其他2个模型,M1和M2模型整体模拟结果相似(图 5e);随着模型序号的增加,NS呈现显著地增加趋势(图 5h);NQ在M2模型整体优于其他2个模型(图 5f);NT随着模型序号的增加而增加,M2和M3模型分布接近且明显优于M1模型(图 5g).
半干旱地区的洪水过程的径流成分主要以地表径流为主,壤中径流和地下径流占比很小. 在采用模型参数进行率定时,发现M1模型(新安江模型)对于这类洪水的模拟存在缺陷,径流深与洪峰两者合格率不能同时保证. 当模拟洪水的径流深合格时,模拟洪水过程是矮胖的,模拟洪峰远远小于实测洪峰;而M3模型(Green-Ampt模型)认为超渗发生在地表,不考虑地下径流,模拟洪水过程线呈现尖瘦的特征,从而模拟径流深更容易合格. 因此,在多目标率定时里,M1模型偏向于“牺牲”径流深合格率,而M3模型倾向于更容易实现的径流深合格,以达到最优的目标值. M2模型(蓄超组合模型)集合了超渗产流和蓄满产流两种机制,具有两个模型共同的优点,中和了单一产流模型在模拟时的倾向性.
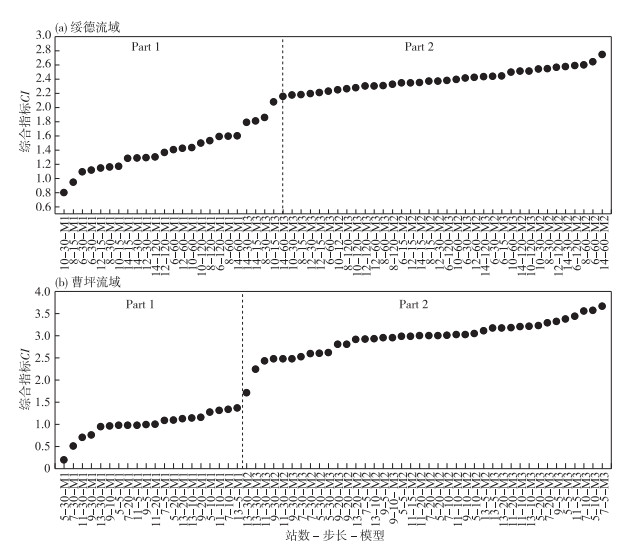
3.2.2 “时—空—模”综合评价结果分析采用公式(7)分别计算绥德和曹坪流域的60个“时—空—模”模拟方案的综合指标,图 6为模拟方案的综合指标结果次序分布. 绥德流域的60个模拟方案的综合指标最大值(2.747)与最小值(0.799)的差值为1.948(图 6a). 曹坪流域60个方案的综合指标最大值(3.665)与最小值(0.199)的差值为3.466(图 6b). 相似的,根据综合指标的升序分布,2个流域的综合指标都很明显分成了2个部分.
|
图 6 绥德流域(a)和曹坪流域(b)的60个“时—空—模”方案模拟结果的综合指标分布情况 Fig.6 Distribution of comprehensive indicators of 60 "time-space-model" simulation schemes in Suide(a) and Caoping(b) Watersheds |
在绥德流域,Part 1阶段有24个“时—空—模”模拟方案,整个阶段呈现快速上升的趋势(图 6a). 很明显,整个阶段由M1模型主导,而雨量站数量的变化没有明显规律,时间步长呈现阶段性增加趋势. Part 2阶段有36个模拟方案,综合指标平稳上升. 前期阶段,M2和M3模型在该阶段交替主导,后期由M2模型主导. 雨量站数量没有明显的分布特征;随着综合指标的增大,时间步长呈现周期性的增减趋势,时间步长较大时,对提升综合指标有明显作用.
在曹坪流域,两个阶段都是先快速后平缓的增长趋势(图 6b). Part 1阶段有20个“时—空—模”模拟方案,整个阶段雨量站数量变化没有明显规律,时间步长逐渐缩短,M1模型占比为100 %. Part 2阶段有40个模拟方案,前期的综合指标快速上升,主导模型不再是M1模型,而是变为M2或者M3模型. Part 2阶段中后期综合指标相比前期增幅减缓,模型完全由M3模型主导,时间步长减小,雨量站数量没有明显的分布特征.
整体来看,在绥德流域(中等流域,资料精度较低),模型和时间步长是对洪水模拟的综合效果影响较大的2个因子. 当模型类别是蓄满产流的M1模型时,不论时间步长和站点数量如何变化,虽然综合模拟效果在快速提升,但是整体模拟效果并没有得到阶段性的跨越,依旧是综合效果较差的部分. 当模型由超渗产流的M3模型主导,模拟综合结果发生跨越性提升;而后由M2模型主导,模拟综合结果继续平稳增长. 这是由于绥德流域面积较大,下垫面空间异质性明显,极易出现多种产流模式混合的情况,此时M2模型灵活的产流结构可以较好地适应该类地区复杂的产流机制. 同时,时间步长的选取对模型模拟效果的影响不能忽略,如绥德流域的观测降雨时间分辨率较低,通过非线性的插值方法,并不能有效改善时间精度,使用较大时间步长反而可以保证模型模拟的综合效果.
在曹坪流域(小流域,资料精度较高),模型是洪水模拟的综合效果影响的主导因子,无论时间步长、雨量站数量怎么组合,M3模型的模拟效果总是趋于较好的结果. 这是因为Green-Ampt模型是点尺度下渗模型,适用于资料丰富的小流域或者实验流域. 对于流域面积很小的曹坪流域,其降雨观测数据的时空分辨率较高,十分符合Green-Ampt模型运行的理想状态,因而模拟精度最高. 因此对于半干旱地区小流域,如果研究区整体数据的时空分辨率较高,可以直接考虑采用M3模型,得到较理想的模拟结果. 然而目前,我国北方中小流域降雨的观测方式主要是自记雨量计与人工记录相结合,存在数据观测记录分辨率不一致和观测设备的稳定性问题,这在一定程度降低了数据分辨率,进而影响模型模拟的结果. 因此,当水文观测不同步且分辨率受限时,步长的设置应以数据观测记录为参照,不宜过分追求较小的时间步长,减少迭代插值的次数.
4 结论本文基于将水文实验和水文模拟技术有机地结合的思想,选择典型中国半干旱地区的实验场区绥德和曹坪流域的观测数据资料,采用降雨相似分形方法和距离平方倒数法,分别从时间和空间维度进行插值处理,设计出不同时空尺度的降雨方案,并作为输入加载至3种不同产流机制的水文模型中进行洪水模拟,去探究时间、空间、产流机制等因素对半干旱地区洪水模拟的影响. 得到了以下主要结论:
1) 半干旱地区中小流域的产流受降雨强度影响大,时间步长越小,降雨方案的精度越高,模型对于洪水过程刻画越精细,模拟的效果越接近真实值. 但在进行降雨等间隔处理时,并不是时间步长越小越好,需要考虑原始资料的观测步长,否则可能出现时间步长越小模拟效果越差的现象. 相比之下,如果流域雨量站的数量能够满足代表性的前提,流域雨量站数量的增减,对于洪水事件的降雨空间分布和量的影响主要是暴雨中心的缺失以及面平均降雨量的微小差别,对洪水模拟效果的影响程度较小.
2) 水文模型能否够准确描述主导水文过程是半干旱地区洪水模拟效果优良的关键. 对于中等流域,由于下垫面空间异质性明显,在洪水形成过程中较易出现多种产流模式混合的情况,随着降雨方案对降雨场描述精准度的提高,蓄超组合模型的模拟效果要优于超渗模型. 相比之下,小流域下垫面空间异质性较弱,无论时间步长、雨量站数量怎么组合,超渗模型的模拟效果总是趋于最好的结果. 因此,针对半干旱地区洪水模拟效果较差的问题,应结合流域尺度和区域下垫面条件,优先考虑从模型结构来调整和发展水文模型.
本研究中重点分析了时间、空间、产流机制等因素对半干旱地区洪水模拟的影响,未来将考虑在不同分辨率的观测数据与具体时间步长的定量的匹配关系和模型参数与尺度之间的关系,进一步发展和完善半干旱地区洪水模拟的研究.
| [1] |
Huang PN, Li ZJ, Yao C et al. Spatial combination modeling framework of saturation-excess and infiltration-excess runoff for semihumid watersheds. Advances in Meteorology, 2016, 2016: 1-15. DOI:10.1155/2016/5173984 |
| [2] |
Li ZJ, Kong XG, Zhang CW. Improving Xin'anjiang model. Hydrology, 1998, 18(4): 20-24. [李致家, 孔祥光, 张初旺. 对新安江模型的改进. 水文, 1998, 18(4): 20-24.] |
| [3] |
Liu YH, Liu ZY, Li ZJ et al. TOKASIDE-D model of spatial dynamic combination of saturation-excess and infiltration-excess runoff for North China region. Journal of Hohai University: Natural Sciences, 2021, 49(2): 105-112. [刘玉环, 刘志雨, 李致家等. 华北地区分布式蓄超空间动态组合TOKASIDE-D模型研究. 河海大学学报: 自然科学版, 2021, 49(2): 105-112.] |
| [4] |
Burns DA, McDonnell JJ, Hooper RP et al. Quantifying contributions to storm runoff through end-member mixing analysis and hydrologic measurements at the Panola Mountain Research Watershed (Georgia, USA). Hydrological Processes, 2001, 15(10): 1903-1924. DOI:10.1002/hyp.246 |
| [5] |
Huang PN, Li ZJ, Chen J et al. Event-based hydrological modeling for detecting dominant hydrological process and suitable model strategy for semi-arid catchments. Journal of Hydrology, 2016, 542: 292-303. DOI:10.1016/j.jhydrol.2016.09.001 |
| [6] |
Li BQ, Niu XR, Liang ZM et al. Progress of research on hydrological models for arid and semi-arid areas of the middle Yellow River. Yellow River, 2017, 39(3): 1-4, 9. [李彬权, 牛小茹, 梁忠民等. 黄河中游干旱半干旱区水文模型研究进展. 人民黄河, 2017, 39(3): 1-4, 9.] |
| [7] |
Al-Qurashi A, McIntyre N, Wheater H et al. Application of the Kineros2 rainfall-runoff model to an arid catchment in Oman. Journal of Hydrology, 2008, 355(1/2/3/4): 91-105. DOI:10.1016/j.jhydrol.2008.03.022 |
| [8] |
Liu XP, Xia CF, Chen ZW et al. A new framework for rainfall downscaling based on EEMD and an improved fractal interpolation algorithm. Stochastic Environmental Research and Risk Assessment, 2020, 34(8): 1147-1173. DOI:10.1007/s00477-020-01823-y |
| [9] |
Wen YH, Li ZJ, Sun MK et al. Influence of rainfall input on real-time flood forecasting accuracy and forecast period. J Lake Sci, 2019, 31(1): 39-51. [温娅惠, 李致家, 孙明坤等. 降雨输入对实时洪水预报精度与预见期的影响. 湖泊科学, 2019, 31(1): 39-51. DOI:10.18307/2019.0104] |
| [10] |
Haberlandt U. Geostatistical interpolation of hourly precipitation from rain gauges and radar for a large-scale extreme rainfall event. Journal of Hydrology, 2007, 332(1/2): 144-157. DOI:10.1016/j.jhydrol.2006.06.028 |
| [11] |
Khodadoust SS, Saghafian B, Moazami S. Comprehensive evaluation of 3-hourly TRMM and half-hourly GPM-IMERG satellite precipitation products. International Journal of Remote Sensing, 2017, 38(2): 558-571. DOI:10.1080/01431161.2016.1268735 |
| [12] |
Huo WB, Li ZJ, Li QL. Hydrological models comparison and ensemble forecasting in semi-humid watersheds. J Lake Sci, 2017, 29(6): 1491-1501. [霍文博, 李致家, 李巧玲. 半湿润流域水文模型比较与集合预报. 湖泊科学, 2017, 29(6): 1491-1501. DOI:10.18307/2017.0621] |
| [13] |
Bao WM, Wang CL. Vertical mixed flow model and its application. Hydrology, 1997, 17(3): 18-21. [包为民, 王从良. 垂向混合产流模型及应用. 水文, 1997, 17(3): 18-21.] |
| [14] |
Li ZJ, Huang PN, Yao C et al. Application of flexible-structure hydrological models in different runoff generation regions. Advances in Water Science, 2014, 25(1): 28-35. [李致家, 黄鹏年, 姚成等. 灵活架构水文模型在不同产流区的应用. 水科学进展, 2014, 25(1): 28-35.] |
| [15] |
Clark MP, Slater AG, Rupp DE et al. Framework for Understanding Structural Errors (FUSE): A modular framework to diagnose differences between hydrological models. Water Resources Research, 2008, 44(12): W00B02. DOI:10.1029/2007WR006735 |
| [16] |
Euser T, Winsemius HC, Hrachowitz M et al. A framework to assess the realism of model structures using hydrological signatures. Hydrology and Earth System Sciences, 2013, 17(5): 1893-1912. DOI:10.5194/hess-17-1893-2013 |
| [17] |
Liu YH, Zhang K, Li ZJ et al. A hybrid runoff generation modelling framework based on spatial combination of three runoff generation schemes for semi-humid and semi-arid watersheds. Journal of Hydrology, 2020, 590: 125440. DOI:10.1016/j.jhydrol.2020.125440 |
| [18] |
Emmanuel I, Andrieu H, Leblois E et al. Influence of rainfall spatial variability on rainfall-runoff modelling: Benefit of a simulation approach?. Journal of Hydrology, 2015, 531: 337-348. DOI:10.1016/j.jhydrol.2015.04.058 |
| [19] |
Douinot A, Roux H, Garambois PA et al. Accounting for rainfall systematic spatial variability in flash flood forecasting. Journal of Hydrology, 2016, 541: 359-370. DOI:10.1016/j.jhydrol.2015.08.024 |
| [20] |
Jie MX. Effects of objective functions and temporal resolutions on hydrological modeling[Dissertation]. Wuhan: Wuhan University, 2017. [揭梦璇. 不同目标函数和时间尺度下水文模拟比较研究[学位论文]. 武汉: 武汉大学, 2017. ]
|
| [21] |
Ostrowski MW, Wolf U. Effects of temporal discretization on parameter estimation for hydrological models. Deutsche Gewasserkundliche Mitteilungen, 1984, 28(2): 37-40. |
| [22] |
Krajewski WF, Lakshmi V, Georgakakos KP et al. A Monte Carlo study of rainfall sampling effect on a distributed catchment model. Water Resources Research, 1991, 27(1): 119-128. DOI:10.1029/90WR01977 |
| [23] |
Wang SP, Zhang ZQ, Sun G et al. Effects of grid size and time step of MIKESHE on hydrological processes modeling at watershed scale. Journal of China Hydrology, 2008, 28(6): 1-7. [王盛萍, 张志强, 孙阁等. 基于物理过程分布式流域水文模型尺度依赖性. 水文, 2008, 28(6): 1-7.] |
| [24] |
Xia J, Ye AZ, Qiao YF et al. An applied research on distributed time-variant gain hydrological model in Wuding river of Yellow River. Journal of Basic Science and Engineering, 2007, 15(4): 457-465. [夏军, 叶爱中, 乔云峰等. 黄河无定河流域分布式时变增益水文模型的应用研究. 应用基础与工程科学学报, 2007, 15(4): 457-465.] |
| [25] |
Hassan SMT, Lubczynski MW, Niswonger RG et al. Surface-groundwater interactions in hard rocks in Sardon Catchment of western Spain: An integrated modeling approach. Journal of Hydrology, 2014, 517: 390-410. DOI:10.1016/j.jhydrol.2014.05.026 |
| [26] |
Zhao RJ. The Xinanjiang model applied in China. Journal of Hydrology, 1992, 135(1/2/3/4): 371-381. DOI:10.1016/0022-1694(92)90096-E |
| [27] |
Heber GW, Ampt GA. Studies on soil phyics. The Journal of Agricultural Science, 1911, 4(1): 1-24. DOI:10.1017/s0021859600001441 |
| [28] |
Liu YH, Li ZJ, Liu ZY et al. Spatial combination model for semi-humid and semi-arid watersheds. J Lake Sci, 2020, 32(3): 826-839. [刘玉环, 李致家, 刘志雨等. 半湿润半干旱流域空间组合模型研究. 湖泊科学, 2020, 32(3): 826-839. DOI:10.18307/2020.0322] |
| [29] |
Duan QY, Sorooshian S, Gupta V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resources Research, 1992, 28(4): 1015-1031. DOI:10.1029/91WR02985 |
| [30] |
National Center of Hydrological Information. Standard for hydrological information and hydrological forecasting. Beijing: China Water Power Press, 2000. [国家水文信息中心. 水文情报预报规范. 北京: 中国水力发电出版社, 2000.]
|
 2022, Vol. 34
2022, Vol. 34 

