(2: 中国地质大学(武汉)环境学院, 武汉 430074)
(3: 江西省水利科学院, 南昌 330029)
(2: School of Environmental Studies, China University of Geosciences, Wuhan 430074, P.R.China)
(3: Jiangxi Provincial Institute of Water Sciences, Nanchang 330029, P.R.China)
较大流域下游洪水通常是由其上游不同来源洪水过程遭遇叠加而成,上下游洪水变量通常具有较强的因果性关联性[1-2],例如,三峡水库入库洪水往往由长江上游与水库区间流域的洪水叠加形成[3]。一般来说,上游不同来源洪水变量,由于其产生的空间接近,气候条件与下垫面条件也较为相似,往往存在一定的相关性,能够反映洪水空间组成规律[4-5]。研究流域不同来源洪水相关性及其下游洪水统计特征的影响有助于科学认识洪水空间组成规律对流域洪水风险的作用机制,对水利水电工程、防洪系统工程设计具有重要的参考价值。
目前关于流域上游不同来源洪水对下游洪水频率分布影响的研究主要集中于设计洪水地区组成[6-9],相关研究通常基于水量平衡原理,假设下游设计断面的洪水变量(通常为洪量)由上游不同来源的洪水变量直接线性叠加而成,因此可以通过不同来源洪水变量和的分布推求设计断面洪量的频率分布。宋松柏等[10]运用Copula函数和数学积分变换原理,假设清江隔河岩水库洪量等于上游水布垭水库洪量加上水-隔区间洪量,严格地推导了二维相依随机变量和概率分布计算公式,并用于研究洪水地区组成。Merz等[11]基于线性叠加的方法由河流干支流交汇点上游站点的洪峰流量频率分布参数推求了下游洪峰流量频率分布参数。上述研究中,下游断面洪水变量一般假设严格等于上游洪水变量的加和,然而实际中考虑到洪水的传播过程,上下游的洪水变量通常不能完全满足该条件,尤其是洪峰流量,往往不能用简单的线性叠加刻画上下游之间关系,现有基于水量平衡的方法适用性受到制约。
广义回归模型可以假设自变量与因变量服从任意概率分布,能够较为灵活地刻画不同随机变量之间的关系,在水文分析中得到广泛应用[12-15]。Jiang等[1]采用广义回归模型刻画上下游洪水变量的关系,基于层次模型由上游洪水频率分布推求了下游洪水频率分布,但该研究并未考虑上游干支洪水变量相关性对下游洪水频率分布的影响。干支流洪水相关性反映了流域不同来源洪水的遭遇规律,然而,现有的研究较少深入分析上游不同来源洪水变量空间相关性对下游洪水频率分布特征的影响。为此,本研究将基于广义回归模型构建上下游洪水变量之间的条件分布,然后采用Copula函数构建河流断面上游干支流洪水变量的联合概率分布,以此刻画流域不同来源洪水的相关性,最后根据全概率公式推导出下游洪水频率分布,在此基础上,将进一步探讨上游干支流洪水变量相关性强度与尾部相关性对下游洪水统计特征及其设计洪水的影响。
1 研究方法 1.1 基于层次模型的洪水频率分布估计假设某水文站位于一条河流干支流交汇点的下游位置,该站点洪水变量定义为Y,交汇点上游两水文站的洪水变量分别定义为X1和X2,具体如图 1所示。
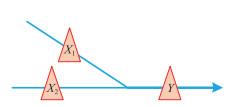
|
图 1 上下游洪水变量空间关系示意 Fig.1 Schematic of the spatial relationship of downstream and upstream flood variables |
为建立上下游洪水频率分布之间关联,本研究基于层次模型由上游干支流洪水的联合概率分布推导下游洪水频率分布[1]。洪水变量Y与上游洪水变量的关系可以由条件分布表示:
| $ Y \mid X_1, X_2 \sim f_{Y \mid X_1, X_2}\left(y \mid x_1, x_2 ; \theta_{Y \mid X_1, X_2}\right) $ | (1) |
式中,x1、x2和y分别为X1、X2和Y的实际观测值,θY|X1, X2为条件分布fY|X1, X2的参数向量,分别包含位置参数μY|X1, X2、尺度参数σY|X1, X2以及形状参数νY|X1, X2(若分布包含该参数)。本研究采用广义回归模型构建条件分布fY|X1, X2参数与上游洪水变量的函数关系,以位置参数μY|X1, X2为例,其表达如下:
| $ \mu_{Y \mid X_1, X_2}=a_0+a_1 x_1+a_2 x_2 $ | (2) |
式中,a0、a1和a2分别为广义回归模型的参数,采用极大似然法估计得到[12]。采用水文频率分析中常用两参数正态分布、对数正态分布、伽马分布、韦伯分布以及三参数皮尔逊Ⅲ型(PⅢ)分布和广义极值(GEV)分布作为条件分布的备选理论分布[1],具体分布表达式如附表Ⅰ所示。采用赤池信息准则(AIC)[12]优选出最优条件分布类型以及参数回归方程。
根据全概率公式,洪水变量Y的频率分布可由下式推导得到:
| $ f_Y(y)=\iint f_{Y \mid X_1, X_2}\left(y \mid x_1, x_2 ; \theta_{Y \mid X_1, X_2}\right) h\left(x_1, x_2\right) \mathrm{d} x_1 \mathrm{~d} x_2 $ | (3) |
式中,h(x1, x2)表示洪水变量X1和X2的联合概率密度函数。根据Casella和Berger[16]的证明,洪水变量Y的期望公式为:
| $ \mathrm{E}(Y)=\mathrm{E}\left(\mathrm{E}\left(Y \mid X_1, X_2\right)\right) $ | (4) |
Y的方差表达式为:
| $ \operatorname{var}(Y)=\mathrm{E}\left(\operatorname{var}\left(Y \mid X_1, X_2\right)\right)+\operatorname{var}\left(\mathrm{E}\left(Y \mid X_1, X_2\right)\right) $ | (5) |
Copula函数可以比较灵活地描述多个水文变量的相关性,在水文领域具有广泛应用[17-20],因此本研究采用Copula函数构建X1和X2的联合概率分布H(x1, x2),如下表示:
| $ H\left(x_1, x_2\right)=C\left[F_{X_1}\left(x_1\right), F_{X_2}\left(x_2\right)\right]=C\left(u_1, u_2\right) $ | (6) |
式中,C(·)表示一个二维Copula函数,FX1(·)和FX2(·)分别表示X1和X2的边缘概率函数,u1和u2分别为x1和x2对应的边缘概率,即u1=FX1(x1)和u2=FX2(x2),均服从区间为[0, 1]的均匀分布。
根据公式(6),X1和X2联合概率密度函数如下表示:
| $ h\left(x_1, x_2\right)=c\left(u_1, u_2\right) \cdot f_{X_1}\left(x_1\right) \cdot f_{X_2}\left(x_2\right) $ | (7) |
式中,c(·)表示Copula函数的概率密度函数,fX1(·)和fX2(·)分别表示X1和X2的概率密度函数。采用我国设计规范[21]推荐的PⅢ型分布作为洪水变量X1和X2的频率分布类型(具体表达式见附表Ⅰ),参数由极大似然法[12]估计得到。
选取Archimedean Copula函数族中的Gumbel Copula、Frank Copula和Clayton Copula构建两变量洪水联合概率分布[17]。为避免边缘分布计算对Copula函数参数θ估计结果的影响,本研究通过计算X1和X2的Kendall相关系数τ,由τ与θ的函数关系(附表Ⅱ)直接估计参数θ。基于理论频率值与实测经验频率值的均方根误差RMSE定量评估Copula函数的拟合效果,并选择拟合效果最佳的Copula函数构建两变量洪水联合概率分布。
1.3 模型求解与分布拟合优度检验理论上,洪水变量Y的频率分布可以通过公式(3)求得,但该公式包含了PⅢ分布以及Copula函数的概率密度函数,难以求得解析解,因此本研究采用蒙特卡洛数值积分方法求解Y的推导频率分布[1]。首先基于Copula函数生成N组边缘概率的随机样本(u1, is, u2, is)(i=1, 2, …, N),并分别代入X1和X2分布的逆函数FX1-1(·)和FX2-1(·)求得N组两变量洪水随机样本(x1, is, x2, is)(i=1, 2, …, N);然后基于广义回归模型结果,将(x1, is, x2, is)代入洪水变量Y条件分布参数的回归方程(公式(2)),最后根据每一组条件分布参数分别生成一个关于洪水变量Y的随机样本yis(i=1, 2, …, N)。对于任意洪水变量观测值y,其累积概率可以通过经验概率公式由随机样本yis(i=1, 2, …, N)推求得到:
| $ F_Y(y)=\frac{1}{N+2} \sum\limits_{i=1}^N 1\left(y_i^s \leqslant y\right) $ | (8) |
洪水频率分布拟合优度采用Kolmogorov-Smirnov(KS)方法进行检验[22],如果检验统计量对应的P值大于某一阈值,则表明洪水频率分布可以通过拟合优度检验。本研究中KS检验P值的阈值取0.05。
2 研究区域与研究数据本文选取抚河流域作为研究区域,抚河位于江西省东部,为全省五大河流之一,也是鄱阳湖主要支流,其主河道长348 km,流域面积16493 km2。抚河下游控制站为李家渡水文站,上游集水面积为15812 km2,占全流域面积的95%以上。李家渡上游干支流交汇点以上分别设有廖家湾水文站和娄家村水文站,控制流域面积分别为8723、4969 km2。抚河流域及其水文站点的空间分布如图 2所示。本研究收集了以上3座水文站1953—2013年间的年最大洪峰流量序列作为研究数据,其中李家渡站、娄家村站和廖家湾站的洪水变量分别定义为Yd、Xc以及Xw。
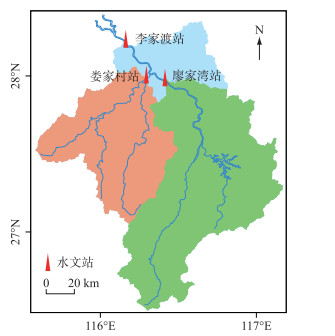
|
图 2 抚河流域及水文站点空间分布 Fig.2 Fuhe River Basin and the spatial distribution of hydrological stations |
基于广义回归模型构建李家渡洪水序列Yd对上游娄家村站和廖家湾站洪水序列(Xw, Xc)条件分布,经过模型比选,伽马分布的AIC值最小,是拟合效果最好的理论分布(附表Ⅲ)。条件分布的位置参数(与期望值相关)与上游干支流洪水变量存在正相关关系,而条件分布的尺度参数为常数。如图 3所示,所选择的条件分布对洪水变量实测值具有较高的拟合程度,95%的分位数区间较窄,这表明李家渡站洪水主要受上游干支流的洪水叠加控制。
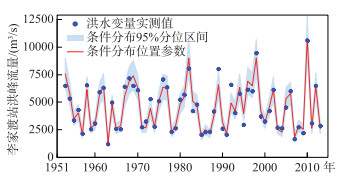
|
图 3 李家渡站洪水变量对上游洪水变量条件分布分位 Fig.3 Quantile plot of the distribution of the flood variable at Lijiadu Station conditioning on upstream flood variables |
采用PⅢ分布分别拟合廖家湾站和娄家村站洪水变量Xw与Xc的边缘分布,参数的极大似然估计结果如表 1所示。结果显示KS检验的P值都超过了0.05,表明PⅢ分布通过了显著性为0.05的拟合优度检验,对Xw与Xc都有很好的拟合效果。由于位于干流的廖家湾站集水面积(8723 km2)要远大于娄家村站的集水面积(4969 km2),因此Xw的均值(2822 m3/s)明显高于Xc的均值(1905 m3/s)。图 4给出了PⅢ分布频率曲线对实测洪水点据的拟合结果,总体来说PⅢ分布对两组洪水序列的拟合较好。
| 表 1 廖家湾站和娄家村站洪水变量频率分布估计结果 Tab. 1 Results of the flood distribution estimation for the flood variables at Liaojiawan and Loujiacun stations |
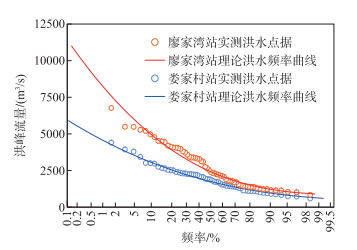
|
图 4 廖家湾站和娄家村站洪水频率曲线拟合结果 Fig.4 Fitted flood frequency curves at Liaojiawan and Loujiacun stations |
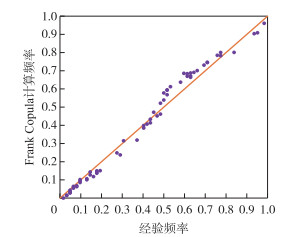
在边缘分布估计的基础上,采用Copula函数构建两变量洪水(Xw, Xc)的联合概率分布,由Kendall相关系数计算Copula函数参数θ。Gumbel、Frank和Clayton三种Copula函数对应的RMSE值分别为0.044、0.038和0.049,很显然Frank Copula对实测序列的拟合效果最好,因此选用该Copula构建(Xw, Xc)的联合概率分布。图 5对比了该Copula函数计算的理论联合概率与经验联合概率,结果表明两者具有较好的吻合程度。
|
图 5 Frank Copula理论频率与经验频率对比 Fig.5 Comparison between theoretical frequency and empirical frequency for Frank Copula |
根据洪水变量(Xw, Xc)的联合概率分布生成100000组随机样本,然后进一步由(Xw, Xc)的随机样本生成100000个李家渡洪水变量Yd的随机样本,并以此来刻画Yd的频率分布。结果显示,推导洪水频率分布的KS检验P值为0.521,能够通过显著性水平为0.05的拟合优度检验,因此由层次模型推求的洪水频率分布具有较好的拟合效果。
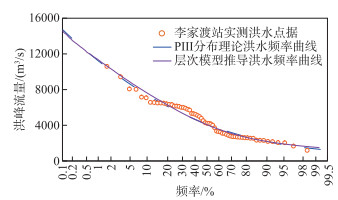
为与理论分布方法相对比,本研究还采用PⅢ分布拟合了李家渡洪水序列的频率分布,结果如表 2所示,总体来说2种方法得到的洪水频率分布统计参数基本一致。图 6对比了PⅢ分布推求的理论洪水频率分布曲线与层次模型推导得到的洪水频率分布曲线,总体来说两者差别不大。需要指出的是蒙特卡洛数值积分方法为一种近似的求解方法,存在一定的计算误差,这导致层次模型推导得到洪水频率分布曲线上尾部分不够平滑。
| 表 2 李家渡站洪水频率分布估计结果 Tab. 2 Results of the flood distribution estimation for the flood variable at Lijiadu Station |
|
图 6 李家渡水文站洪水频率曲线拟合结果 Fig.6 Fitted flood frequency curves at Lijiadu Station |
如公式(3)所示,下游洪水变量的频率分布取决于上下游洪水变量之间的条件分布与上游洪水变量的联合分布。根据前文结果,下游李家渡站洪水变量条件分布为伽马分布,其位置参数μYd|Xw, Xc即为条件分布期望值E(Yd|Xw, Xc)。李家渡洪水变量均值E(Yd)有如下理论表达式:
| $ \mathrm{E}\left(Y_{\mathrm{d}}\right)=\mathrm{E}\left(\mathrm{E}\left(Y_{\mathrm{d}} \mid X_{\mathrm{w}}, X_{\mathrm{c}}\right)\right)=\mathrm{E}\left(a_0+a_1 X_{\mathrm{w}}+a_2 X_{\mathrm{c}}\right)=a_0+a_1 \mathrm{E}\left(X_{\mathrm{w}}\right)+a_2 \mathrm{E}\left(X_{\mathrm{c}}\right) $ | (9) |
式中, E(Xw)和E(Xc)分别为廖家湾站与娄家村站洪水变量的均值。李家渡洪水变量的方差var(Yd)有如下理论表达式:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\; \operatorname{var}\left(Y_{\mathrm{d}}\right)=\mathrm{E}\left(\operatorname{var}\left(Y_{\mathrm{d}} \mid X_{\mathrm{w}}, X_{\mathrm{c}}\right)\right)+\operatorname{var}\left(\mathrm{E}\left(Y_{\mathrm{d}} \mid X_{\mathrm{w}}, X_{\mathrm{c}}\right)\right)= \\ \mathrm{E}\left({\sigma_{Y_{\mathrm{d}} \mid X_{\mathrm{w}}, X_{\mathrm{c}}{ }}}^2 \cdot\left[a_0+a_1 X_{\mathrm{w}}+a_2 X_{\mathrm{c}}\right]^2\right)+\operatorname{var}\left(a_0+a_1 X_{\mathrm{w}}+a_2 X_{\mathrm{c}}\right)= \\ {\sigma _{{Y_{\rm{d}}}\mid {X_{\rm{w}}},{X_{\rm{c}}}}}^2 \cdot \left\{ \begin{array}{l} {\rm{E}}\left( {a_0^2} \right) + a_1^2{\rm{E}}\left( {X_{\rm{w}}^2} \right) + a_2^2{\rm{E}}\left( {X_{\rm{c}}^2} \right) + 2{a_0}{a_1}{\rm{E}}\left( {{X_{\rm{w}}}} \right) + 2{a_0}{a_2}{\rm{E}}\left( {{X_{\rm{c}}}} \right)\\ + 2{a_1}{a_2}\left[ {{\rm{E}}\left( {{X_{\rm{w}}}} \right) \cdot {\rm{E}}\left( {{X_{\rm{c}}}} \right) + {\mathop{\rm cov}} \left( {{X_{\rm{w}}},{X_{\rm{c}}}} \right)} \right] + \end{array} \right\} + \\ a_1^2{\mathop{\rm var}} \left( {{X_{\rm{w}}}} \right) + a_2^2{\mathop{\rm var}} \left( {{X_{\rm{c}}}} \right) + 2{a_1}{a_2}{\mathop{\rm cov}} \left( {{X_{\rm{w}}},{X_{\rm{c}}}} \right) \end{array} $ | (10) |
式中,var(Xw)和var(Xc)分别为廖家湾站与娄家村站洪水变量的方差,cov(Xw, Xc)为上述两个洪水变量的协方差。从公式(9)和(10)可以看出Yd的均值仅取决于上游两变量洪水Xw和Xc的均值,Yd的方差(或Cv)除与廖家湾站与娄家村站洪水变量各自统计特征值有关外,还受两者协方差cov(Xw, Xc)的控制,即Xw和Xc之间的相关性。
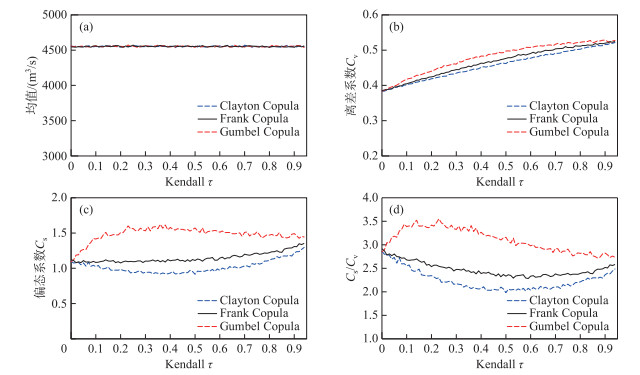
为进一步探讨上游干支流洪水变量相关性对下游李家渡站洪水变量统计特征及其洪水设计值的影响,本研究基于Frank Copula函数参数θ与Kendall相关系数τ的函数关系(附表Ⅱ),生成τ不同取值条件下Yd的频率分布。图 7给出Yd统计特征值随(Xw, Xc)相关系数τ的变化,由于蒙特卡洛数值积分存在一定误差,Yd统计特征值存在一定的随机波动,但可以明显看出Yd分布的均值基本不随τ的变化而变化,而Cv值随着τ的增大呈现非常明显的增加趋势,上述发现与公式(9)和(10)的结果一致。如图 7b所示,当(Xw, Xc)的Kendall相关系数τ为0时,Yd分布的Cv值约于0.385,而当τ为0.9时, Cv值增加至0.520。(Xw, Xc)相关性对Cs值的影响相对较小,当τ小于0.5时,Cs值基本没有变化,而当τ超过0.5时,Cs随相关性的增强而增大。
|
图 7 上游两变量洪水相关性对下游李家渡站洪水变量频率分布特征影响 Fig.7 Impacts of the correlation between the upstream bivariate flood variables on the flood frequency distribution at Lijiadu Station |
除了相关性强度,进一步探讨上游洪水变量(Xw, Xc)尾部相关性对下游洪水频率分布的影响。不同Copula函数对尾部特征的刻画差别较大[17],例如Gumbel Copula侧重上尾相关性,Clayton Copula侧重下尾相关性,而Frank Copula的上、下尾相关系数相等且都为零,因此将分别基于上述3种Copula函数生成廖家湾站与娄家村站洪水变量的随机样本,在此基础上分别推求李家渡站洪水变量Yd对应的频率分布。不同Copula函数对应的洪水频率分布统计特征值对比如图 7所示,可见(Xw, Xc)尾部相关性对李家渡站洪水频率分布的均值没有影响,但对高阶参数Cv和Cs影响较为显著,尤其是相关系数τ介于0.1~0.8之间时。从图 7b可以看出,Gumbel Copula函数侧重上尾相关性,由该函数生成的李家渡站洪水频率分布Cv值最大,其次为无尾部相关性的Frank Copula,侧重下尾相关的Clayton Copula函数得到Cv值最小,偏态系数Cs也呈现类似的对比结果(图 7c)。同时还可以看出,尾部相关性对Cs的总体影响程度甚至要明显超过相关性强度。同时,还可以发现在上游洪水变量相关性极弱或极强的情况下,尾部相关性的差异对下游洪水频率分布的Cv和Cs的影响都不再明显。上述发现表明流域上游不同来源洪水发生的空间相关性强度与尾部相关性都是影响下游洪水频率分布规律的重要因素。
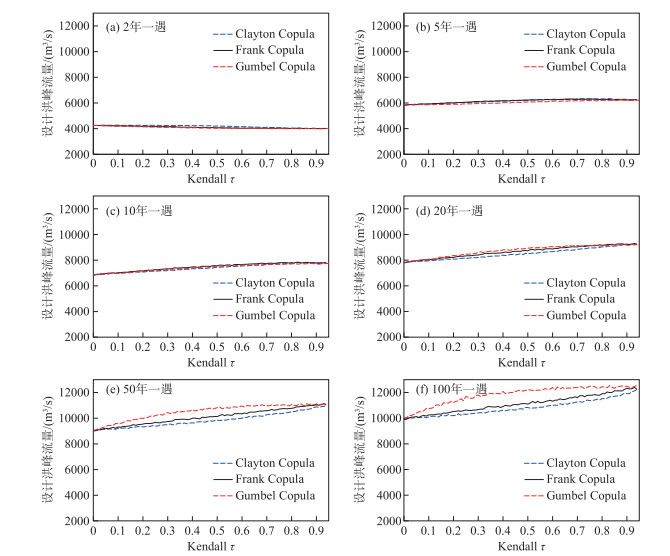
图 8给出了上游廖家湾和娄家村站洪水变量(Xw, Xc)相关性对不同重现期下李家渡站设计洪峰流量的影响,从中可以看出,上游洪水变量相关性强度变化对下游不同重现期设计洪水的影响有所不同。随着上游洪水变量(Xw, Xc)相关性增强,下游李家渡站2年一遇的设计洪水值呈现微弱的减小趋势,τ=0.9对应的设计值较τ=0的设计值减小了约240 m3/s,而对于5年及以上重现期,李家渡站水文设计值随(Xw, Xc)相关性增强呈现增加趋势,且靠近上尾部分(重现期较长)的极端水文设计值对(Xw, Xc)相关性变化更为敏感,随着(Xw, Xc)的相关系数τ由0增加至0.9,5、10、20、50、100年一遇的设计洪水增加幅度分别为400、900、1400、2000、2300 m3/s,相对增加幅度分别为7%、13%、18%、22%、24%。上游洪水变量(Xw, Xc)相关性越强意味着上游洪水的发生越趋向于同频率,上述结果进一步表明,流域内不同来源洪水的发生规律越趋向于同频率,流域的极端洪水风险就越高。
|
图 8 上游两变量洪水相关性对下游李家渡站水文设计值的影响 Fig.8 Impact of the correlation between the upstream bivariate flood variables on the hydrological design values at Lijiadu Station |
如图 8所示,随着重现期的变长,上游洪水变量(Xw, Xc)尾部相关性对李家渡站水文设计值的影响越来越显著。当设计值重现期超过50年后,侧重上尾相关的Gumbel Copula函数对应的水文设计值要显著大于无尾部相关性Frank Copula函数以及侧重下尾相关性Clayton Copula函数对应的水文设计值。上游洪水变量上尾相关性越强意味着同时发生极端洪水事件的可能性越高,相应的下游洪水极端洪水风险也就越高。因此,在极端水文事件分析中,尾部相关性对水文风险的刻画与计算具有不可忽略的作用。从图 8同样可以看出,在上游洪水变量相关性极弱或极强的情况下,尾部相关性的差异对下游水文设计值的影响不再显著。
4 结论与讨论为研究上游不同来源洪水相关性对下游洪水频率分布特征的影响,选取鄱阳湖支流抚河流域作为研究区,基于层次模型由上游干支流洪水变量的联合概率分布推求了下游洪水频率分布,并探讨了上游洪水变量相关性强度以及尾部相关性对下游洪水统计特征的影响。主要研究结论为:由层次模型推导得到的抚河下游李家渡站洪水频率分布有较好的拟合效果,与传统的PⅢ分布拟合的频率曲线基本相当;上游不同来源洪水相关性是影响下游洪水频率分布的重要因素,理论公式推导与数值实验结果都表明,上游洪水变量相关性强度与尾部相关性对下游洪水频率分布均值没有影响,但均对高阶统计参数有明显的影响,下游洪水频率分布的Cv值会随上游洪水变量相关性的增强而显著增大,上尾相关性越强Cv和Cs越大,对应的流域洪水极端洪水风险也就越高;流域极端洪水设计值对流域不同来源洪水相关性强度及尾部相关性的变化更加敏感。
现有的设计洪水地区组成研究方法假定下游断面洪量为上游断面与区间洪量的加和,需要指出的是该假设仅适用于相应洪量情景,忽略了洪水的传播过程,这与实际情况并不完全相符,且无法用于洪峰的地区组成。本文采用的广义回归模型可以灵活描述上下游洪水变量的线性与非线性关系,为解决上述问题提供了一种可行的途径。此外,上游洪水变量作为下游洪水变量具有物理成因机制的解释变量,在上游的洪水序列的观测期长于下游的情况下,引入上游更长洪水样本信息可有效提高下游洪水频率分布估计成果的稳健性[5],本文采用的层次模型可以为上述思路的实现提供方法支撑[23]。
本文提出的基于层次模型的洪水频率分布推求方法依赖于上下游洪水变量之间的条件分布、Copula函数、上游洪水频率分布的估计结果,另一方面,采用的蒙特卡洛数值积分为一种近似的求解方法,也存在一定的计算误差,上述因素对洪水频率分布估计成果的不确定性有待进一步深入研究。
5 附录附表Ⅰ~Ⅲ见电子版(DOI: 10.18307/2024.0453)。
| 附表Ⅰ 本研究采用的条件分布表达式 Appendix Ⅰ Conditional distributions used in this study |
| 附表Ⅱ 本研究采用的Archimedean Copula函数表达式 Appendix Ⅱ Three types of Archimedean Copula used in this study |
| 附表Ⅲ 抚河上下游洪水变量条件分布拟合结果对比 Appendix Ⅲ Comparison of the fitting quality for the conditional distributions of |
| [1] |
Jiang C, Xiong L, Xu CY et al. A river network-based hierarchical model for deriving flood frequency distributions and its application to the upper Yangtze basin. Water Resources Research, 2021, 57(8): e2020WR029374. DOI:10.1029/2020WR029374 |
| [2] |
Peng Y, Chen K, Yan HX et al. Improving flood-risk analysis for confluence flooding control downstream using Copula Monte Carlo method. Journal of Hydrologic Engineering, 2017, 22(8): 04017018. DOI:10.1061/(asce)he.1943-5584.0001526 |
| [3] |
Liu DY, Zhang MB. Analysis of flood composition in upper stream of TGP. Yangtze River, 2010, 41(19): 14-17. [刘冬英, 张明波. 长江三峡以上洪水组成分析. 人民长江, 2010, 41(19): 14-17.] |
| [4] |
Lu WW, Chen L, Zhou JZ et al. Regional flood frequency analysis based on multivariate distribution function. Journal of China Hydrology, 2015, 35(5): 6-10. [卢韦伟, 陈璐, 周建中等. 基于多元分布函数的区域洪水频率分析. 水文, 2015, 35(5): 6-10. DOI:10.3969/j.issn.1000-0852.2015.05.002] |
| [5] |
Merz R, Blöschl G. Flood frequency hydrology: 1. Temporal, spatial, and causal expansion of information. Water Resources Research, 2008, 44(8): W08432. DOI:10.1029/2007wr006744 |
| [6] |
Huang N. A numerical method for computing the combinatorial frequency of the sum of two gamma distributed random variables independent of each other. Journal of Hefei University of Technology: Natural Science, 1987, 10(5): 110-116. [黄农. 一种推算两独立Г分布随机变数之和的组合频率数值计算法. 合肥工业大学学报: 自然科学版, 1987, 10(5): 110-116.] |
| [7] |
Yan BW, Guo SL, Guo J et al. Regional design flood composition based on Copula function. Journal of Hydroelectric Engineering, 2010, 29(6): 60-65. [闫宝伟, 郭生练, 郭靖等. 基于Copula函数的设计洪水地区组成研究. 水力发电学报, 2010, 29(6): 60-65.] |
| [8] |
Liu ZJ, Guo SL, Li TY et al. General formula derivation of most likely regional composition method for design flood estimation of cascade reservoirs system. Advances in Water Science, 2014, 25(4): 575-584. [刘章君, 郭生练, 李天元等. 梯级水库设计洪水最可能地区组成法计算通式. 水科学进展, 2014, 25(4): 575-584.] |
| [9] |
Li TY, Guo SL, Liu ZJ et al. Design flood estimation methods for cascade reservoirs. Journal of Hydraulic Engineering, 2014, 45(6): 641-648. [李天元, 郭生练, 刘章君等. 梯级水库下游设计洪水计算方法研究. 水利学报, 2014, 45(6): 641-648.] |
| [10] |
Song SB, Wang XJ. Probability distribution calculation of the sum of hydrological random variables based on Copula function approach. Journal of Hydraulic Engineering, 2018, 49(6): 687-693. [宋松柏, 王小军. 基于Copula函数的水文随机变量和概率分布计算. 水利学报, 2018, 49(6): 687-693.] |
| [11] |
Merz R, Blöschl G. Flood frequency hydrology: 2. Combining data evidence. Water Resources Research, 2008, 44(8): W08433. DOI:10.1029/2007wr006745 |
| [12] |
Rigby RA, Stasinopoulos DM. Generalized additive models for location, scale and shape. Journal of the Royal Statistical Society Series C: Applied Statistics, 2005, 54(3): 507-554. DOI:10.1111/j.1467-9876.2005.00510.x |
| [13] |
Liang ZM, Hu YM, Wang J. Advances in hydrological frequency analysis of non-stationary time series. Advances in Water Science, 2011, 22(6): 864-871. [梁忠民, 胡义明, 王军. 非一致性水文频率分析的研究进展. 水科学进展, 2011, 22(6): 864-871.] |
| [14] |
Villarini G, Smith JA, Serinaldi F et al. Flood frequency analysis for nonstationary annual peak records in an urban drainage basin. Advances in Water Resources, 2009, 32(8): 1255-1266. DOI:10.1016/j.advwatres.2009.05.003 |
| [15] |
López J, Francés F. Non-stationary flood frequency analysis in continental Spanish Rivers, using climate and reservoir indices as external covariates. Hydrology and Earth System Sciences, 2013, 17(8): 3189-3203. DOI:10.5194/hess-17-3189-2013 |
| [16] |
Casella G, Berger RL. Statistical inference (second edition). USA: Thomson Learning, 2001, 162-168. |
| [17] |
Song SB. Discussion on application Copula functions to multivariate hydrological analysis calculation. Yellow River, 2019, 41(10): 40-47, 57. [宋松柏. Copula函数在水文多变量分析计算中的问题. 人民黄河, 2019, 41(10): 40-47, 57. DOI:10.3969/j.issn.1000-1379.2019.10.008] |
| [18] |
Liu ZJ, Guo SL, Xu XF et al. Application of Copula functions in hydrology and water resources: A state-of-the-art review. Advances in Water Science, 2021, 32(1): 148-159. [刘章君, 郭生练, 许新发等. Copula函数在水文水资源中的研究进展与述评. 水科学进展, 2021, 32(1): 148-159.] |
| [19] |
Sun P, Zhang Q, Chen XH. Copula-based evaluation of high-and low-flows frequency of the Lake Poyang Basin and the risk assessment. J Lake Sci, 2011, 23(2): 183-190. [孙鹏, 张强, 陈晓宏. 基于Copula函数的鄱阳湖流域极值流量遭遇频率及灾害风险. 湖泊科学, 2011, 23(2): 183-190. DOI:10.18307/2011.0204] |
| [20] |
Luo Y, Dong ZC, Guan XK et al. Flood risk analysis in the Taihu Basin during flood periods based on Copula function. J Lake Sci, 2020, 32(1): 223-235. [罗赟, 董增川, 管西柯等. 基于Copula函数的太湖流域汛期洪涝灾害危险性分析. 湖泊科学, 2020, 32(1): 223-235. DOI:10.18307/2020.0121] |
| [21] |
中华人民共和国水利部. 水利水电工程设计洪水计算规范: SL 44—2006. 北京: 中国水利水电出版社, 2006.
|
| [22] |
Jr Massey FJ. Thekolmogorov-smirnov test for goodness of fit. Journal of the American Statistical Association, 1951, 46(253): 68-78. DOI:10.1080/01621459.1951.10500769 |
| [23] |
Jiang C, Xiong LH, Huang JZ et al. A derivation method of flood frequency distribution incorporating rainfall stochastic variable. Journal of Hydraulic Engineering, 2023, 54(1): 45-53. [江聪, 熊立华, 黄俊哲等. 融合降雨随机变量的洪水频率分布估计方法研究. 水利学报, 2023, 54(1): 45-53.] |
 2024, Vol. 36
2024, Vol. 36 

