基于概念性水文模型与长短时记忆模型耦合的汉江上游流域径流模拟
doi: 10.18307/2025.0143
邓超1,2 ， 孙培源1,2 ， 尹鑫3 ， 邹佳成4 ， 王卫光1,2
1. 河海大学水文水资源学院，南京 210098
2. 河海大学，水灾害防御全国重点实验室，南京 210098
3. 南京水利科学研究院，水灾害防御全国重点实验室，南京 210029
4. 赣江下游水文水资源监测中心，宜春 336000
基金项目: 国家重点研发计划项目（2022YFC3202802） ； 国家自然科学基金项目（51979071）联合资助
Runoff simulation in the upper Han River Basin using physics-informed machine learningmodel
Deng Chao1,2 ， Sun Peiyuan1,2 ， Yin Xin3 ， Zou Jiacheng4 ， Wang Weiguang1,2
1. College of Hydrology and Water Resources, Hohai University, Nanjing 210098 , P.R.China
2. The National Key Laboratory of Water Disaster Prevention, Hohai University, Nanjing 210098 , P.R.China
3. The National Key Laboratory of Water Disaster Prevention, Nanjing Hydraulic Research Institute, Nanjing 210029 , P.R.China
4. Hydrology and Water Resources Monitoring Center of Lower Ganjiang River, Yichun 336000 , P.R.China
摘要
为了探究概念性水文模型（GR4J）与长短时记忆模型（LSTM）耦合过程中物理模型参数反馈机制以及考虑土壤含水量作为中间变量对物理引导机器学习（PIML）模型径流模拟的影响，本研究构建了PIML模型并设置考虑参数反馈、考虑中间变量和两者同时考虑的3种方案（依次简称为H1、H2、H3），以安康站为控制站的汉江上游流域开展实例研究。结果表明：（1）3种PIML模型径流模拟效果均优于LSTM模型，其中验证期纳什系数（NSE）平均提升10.6%，而PIML-H1与PIML-H3模型径流模拟效果优于GR4J模型，验证期NSE平均提升4.2%，其中PIML-H3模型在3种PIML模型中表现最佳，表明基于LSTM和GR4J模型构建的PIML模型对径流模拟效果有所改善，且同时考虑中间变量和参数反馈因素时对径流模拟效果改善最佳；（2）3种PIML模型对低水流量的模拟效果均优于GR4J和LSTM模型，且PIML-H3模型效果最佳，而对于高水流量，3种PIML模型均表现不佳，说明PIML模型往往在模拟低流量事件中更占优势；（3）3种PIML模型的径流模拟效果均表现出较强的季节性变化，PIML-H2和PIML-H3模型相较于PIML-H1模型受到的季节性变化影响更为明显，说明PIML模型模拟径流结果的季节性变化受到中间变量的影响。研究可为汉江上游流域径流模拟预报提供技术支撑。
Abstract
This study investigated the impact of coupling the conceptual hydrological model (GR4J) with the long short-term memory model (LSTM) in a physics-informed machine learning (PIML) framework for runoff simulation. Three scenarios (H1, H2 and H3) were designed to examine the effects of the physical model parameter feedback mechanism, the consideration of soil moisture as an intermediate variable, and the former both on the PIML models, respectively. The case study was conducted in the upper Han River Basin, with the Ankang hydrological station as the control station. The main findings were as follows: (1) Compared with the LSTM model, all three PIML models had improved performance on runoff simulation, with a 10.6% increase in average Nash-Sutcliffe efficiency (NSE) during the validation period. Additionally, both the PIML-H1 and PIML-H3 models exhibited better performance than the GR4J model, with a 4.2% increase in average NSE during the validation period. Notably, the PIML-H3 model outperformed other PIML models, indicating that coupling GR4J and LSTM models simultaneously considering intermediate variables and parameter feedback yielded the most significant improvement in the model performance of runoff simulation. (2) For low flows, all three PIML models outperformed the GR4J and LSTM models, and the PIML-H3 model achieved the best performance. For high flows, the performance of all three PIML models was not high, implying that PIML models were suitable in simulating low flows events. (3) The runoff simulations from the three PIML models exhibited significantly seasonal variations during both the training and validation periods. The seasonal variations in the PIML-H2 and PIML-H3 models were more pronounced compared to that in the PIML-H1 model, indicating that the seasonal variations in simulated runoff results of the PIML model were influenced by intermediate variables. This study contributed to a better understanding of the performance differences among various PIML model schemes in runoff simulation, providing technical support for runoff simulation and forecasting in the study area.
近年来，受气候变化和高强度人类活动共同影响，极端水文事件发生频次及量级远超历史，流域水安全和水资源管理问题更加突出[1]。我国政府明确提出要以全面提升水安全保障能力为目标，完善流域防洪减灾体系为重点。径流模拟与流域防洪减灾、水资源管理等密切相关，一直以来都是流域水文学的关键任务[2-6]。作为流域径流模拟的重要工具，流域水文模型通常可分为两类：基于物理概念的模型和基于数据驱动的模型[7]。相较于物理概念模型，数据驱动模型由于计算复杂性低且模型精度高，已广泛用于径流模拟预报[8]，尤其是机器学习（machine learning，ML）模型，如极端梯度提升（extreme gradient boosting，XGBoost）、循环神经网络（recurrent neural network，RNN）、长短时记忆模型（long short-term memory model，LSTM）[8-9]。近年来，利用LSTM开展流域径流模拟得到了广泛的应用与验证[10-12]。然而，由于其“黑箱”性质，模型仅考虑输入、输出变量之间的统计学关系而忽略了流域水文过程的物理机制[13]，使得模型结果存在过度拟合以及过程缺乏解释性等问题[14]。
针对ML模型存在的上述问题，许多学者将物理模型和机器学习耦合开展水文模拟预报研究[15-16]。物理引导机器学习（physics-informed machine learning，PIML）作为一种耦合方法，能够结合物理模型对流域水文过程机理的概化描述和ML模型的数据挖掘能力，通过将已知的物理定律或规律整合到ML中，并对ML模型的输出进行约束或限制从而提高预测的稳定性，该类方法已经在降雨径流预测中得到有效应用[17-18]。目前，常用的PIML方法是将基于物理模型得到的输出结果（如模拟流量，水文中间变量）作为ML模型的输入[19-21]，或构建独立的参数通道以耦合物理模型与ML模型[17]。例如，Yu等[22]将HBV水文模型与LSTM模型相结合，考虑了LSTM模型和HBV模型之间的参数反馈，但其训练机器学习模型的输入信息中未考虑水文中间变量（如蒸散发、土壤含水量）对径流过程的影响。水文中间变量作为降雨和径流之间的桥梁，充分考虑其对径流的影响有助于增强有效信息的利用，进而提高ML模型模拟的稳定性和精准度[23-24]。Bhasme等[25]提出的PIML方案将概念性水文模型与机器学习算法相结合，通过概念性水文模型提取的变量函数关系确定ML模型输入来先后预测中间变量（即实际蒸散发）和目标变量（即径流），该方法考虑了中间变量对径流预测的影响。但在构建PIML模型时，概念水文模型与ML模型之间的直接反馈联系在该框架中尚未得到充分探讨。此外，考虑中间变量影响的GR4J模型和ML模型耦合的问题研究尚缺乏。
因此，本研究基于概念性水文模型（Génie Ruralà 4 paramètres Journalier，GR4J）与LSTM模型构建PIML模型，考虑了GR4J与LSTM模型的参数反馈以及中间状态变量对于PIML模型构建的影响，通过设置3种不同PIML方案，以汉江上游流域开展流域日径流模拟研究。
1 数据资料
1.1 流域概况
汉江作为长江最大的支流，全长1577 km。其发源地位于陕西省宁强县冢山，流域横跨湖北、陕西、甘肃、四川、重庆5个省（市），总面积达15.9万km2[26-27]。本文以安康水文站为控制站的汉江上游流域为研究对象，该站点位于陕西省安康市汉滨区，地理坐标为33.67°N，109°E（图1），以安康站为控制站的集水面积达3.98万km2，占据整个汉江流域总面积的25%。该地区北靠秦岭，南与大巴山相接，地势两边高、中间低，属于亚热带湿润性季风气候。受秦岭、巴山的影响，该地区同时兼有暖湿带和中温带山地气候特征，四季分明，雨量充沛，无霜期长，多年平均年降水量为976 mm，年平均潜在蒸发量为897 mm，年平均径流深为446 mm[28]。此外，该地区历史上植被覆盖面积广，以常绿落叶阔叶混交林为主。由于该地区气温较高，降水较多，岩石的物理、化学风化和溶蚀作用也比较强烈，在缓坡地带形成了厚厚的松散坡积物和棕黄色的亚黏土堆，形成重力地貌。
1.2 数据来源与处理
研究使用的数据主要包括地面观测数据和遥感数据。
地面观测数据包括流量和气象数据。其中流量资料来源于水文年鉴安康水文站的实测逐日平均流量。气象数据包括降水（P）、温度、相对湿度、日照时速、气压、风速，该数据来源于国家气象科学数据中心（https://data.cma.cn）。因考虑到数据质量以及数据序列的连续性，选取了汉江上流流域内及相邻11个气象站点（图1）的逐日观测数据。
图1汉江上游流域地理位置及气象站、水文站分布
Fig.1Location of the upper Han River Basin and the distribution of meteorological and hydrological stations
遥感数据为逐日土壤含水量（S）数据，该数据来源于美国国家航空航天局全球陆地数据同化系统（global land data assimilation system，GLDAS）的卫星数据产品。本文采用的数据为GLDAS-2.1版本，序列起止时间为2000年至今，时间分辨率为3 h，空间分辨率为0.25°，来源于https://doi.org/10.5067/G90R32A924YM。研究区的面平均逐日土壤含水量基于流域边界并采用Google Earth Engine（https://earthengine.google.com/）提取得到，其中面平均方法采用空间数据的区域统计方法，使用GEE中自带的reduceRegion函数，且函数reducer属性设置为Reducer.mean。
此外，根据水文模型输入数据要求，潜在蒸散发（PET）数据根据已有气象资料采用彭曼-蒙特斯（Peman-Monteith）[29]公式计算得出。考虑到降水、潜在蒸散发以及土壤含水量与径流数据在时间序列上的匹配性及数据质量，本文选取2000年1月1日和2011年12月31日作为本次研究的数据序列起止时间。
2 研究方法
2.1 GR4J模型
GR4J模型[30]是一个集总式概念性水文模型，其采用两个非线性水库来模拟产流和汇流过程，模型输入为日降水P（mm）和日潜在蒸散发PET（mm）两部分。该模型已广泛应用于国内外湿润、半湿润地区的径流模拟与预报中[31-32]。该模型仅有4个参数，分别为产流水库最大容量x1（mm）、地下水交换系数x2（mm）、汇流水库最大容量x3（mm）、单位线汇流时间x4（d）。
2.2 LSTM模型
LSTM模型是由Hochreiter和Schmidhuber[33]在1997年首次提出的一种特殊类型的循环神经网络（RNN），该模型广泛应用于基于时间序列数据的分类、处理和预测[34]。与RNN相比，LSTM在隐藏层中添加了一个记忆单元，取代了RNN中的原始单元，可以对带有时间段的序列数据进行特征提取，克服了RNN的梯度爆炸和消失弱点[35]。本文中使用的单一LSTM模型结构采用两层LSTM层，隐藏层为一层，Dropout层数为两层。LSTM模型结构可由以下方程描述：
ft=σWf⋅ht-1,xt+bf
(1)
it=σWi⋅ht-1,xt+bi
(2)
C~t=tanh⁡WC⋅ht-1,xt+bC
(3)
Ct=ft×Ct-1+it×C~t
(4)
Ot=σW0⋅ht-1,xt+b0
(5)
ht=Ot×tanh⁡Ct
(6)
式中，t表示时间步长；xt为输入到LSTM单元的输入向量；ft为遗忘门的激活向量；it为输入门的激活向量；Ot为输出门的激活向量；ht为隐藏状态向量，也称为LSTM单元的输出向量；C~t为细胞输入激活向量；Ct为细胞状态向量；W和b为需要在训练过程中更新的权重矩阵和偏差向量参数。
2.3 PIML模型
本文采用的PIML模型框架由Bhasme等[20]提出，其实质是从概念性物理水文模型中提取水文变量之间的关系，随后用于确定基于ML模型预测目标变量的输入。本研究基于GR4J与LSTM模型构建PIML模型，并分别设置了考虑参数反馈、考虑中间变量和两者同时考虑共3种方案（依次简称为H1、H2、H3），各方案流程如图2所示。
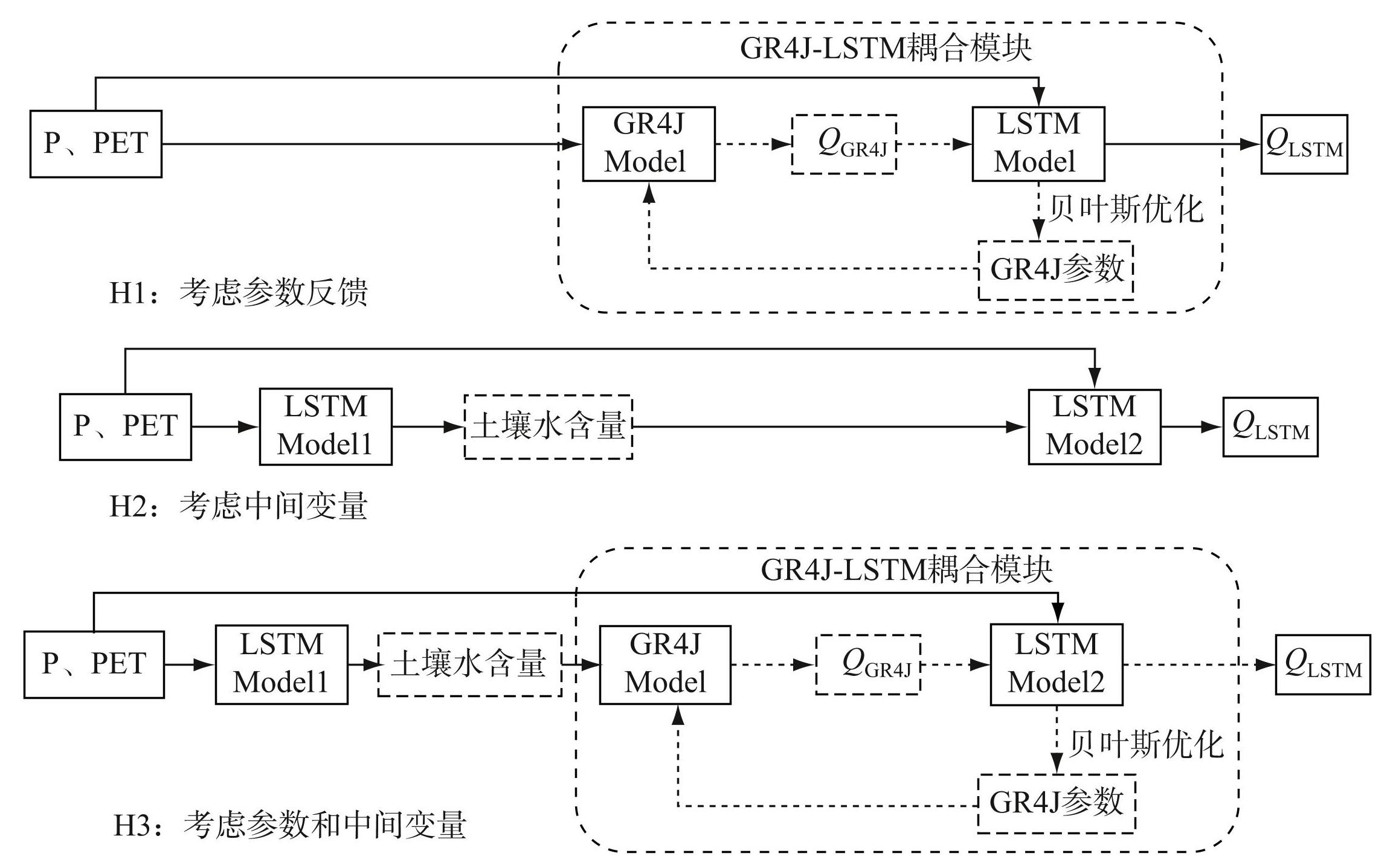
图23种PIML模型方案流程
Fig.2The architectural framework of three scenarios of PIML model
H1方案考虑了GR4J模型与LSTM模型之间的输入输出反馈；H2方案中，根据产汇流原理，通过采用两层ML模型来考虑中间变量的约束作用；H3方案则是一种综合考虑参数变量和中间变量的方案。3种PIML模型方案的原始输入包括降水和潜在蒸散发。
在H1方案中，建立GR4J模型和LSTM模型的耦合模块。该模块的输入包括P、PET，输出为LSTM模型的模拟流量QLSTM，其中GR4J模型的模拟流量QGR4J被视为中间变量。在此过程中，采用贝叶斯优化算法对LSTM模型的超参数和GR4J模型的参数进行调优。调优过程中设置初始的GR4J模型参数集（x1、x2、x3、x4）以及LSTM的超参数，并在取值范围内迭代搜索使得模型性能最优的参数组合。当前迭代过程得到新的最优GR4J模型参数集（x11、x12、x13、x14）将会替换原参数以生成QGR4J1。更新后的GR4J模型将再次与LSTM模型耦合，LSTM模型以P、PET和新的QGR4J1作为输入，生成QLSTM1。通过对GR4J模型参数不断更新实现参数反馈，直至搜寻到满足QLSTM模拟最优条件下的参数组合，并输出最优径流模拟结果。
H2方案是通过从GR4J模型中提取的变量函数关系来确定LSTM模型的输入来先后预测中间变量（土壤含水量）和目标变量（即径流），该方法考虑了中间变量对径流预测的影响。
在H2和H3方案中，降水和潜在蒸散发数据首先输入到第一层LSTM模型模拟中间变量，随后，中间变量、降水和潜在蒸散发一并输入到下一层LSTM模型中；在两个方案中，GR4J模型的中间变量土壤水含量计算模块用ML模型替换。H2和H3两个方案的不同之处在于，H2的中间变量和原始输入被代入第二层LSTM模型，而H3则将其代入GR4J模型中，其余的过程与H1相似。
本研究基于GR4J、LSTM、PIML-H1、PIML-H2、PIML-H3 5种水文模型进行汉江上游流域的日径流模拟，各模型的输入输出变量如表1所示。GR4J模型参数率定基于Python 3.10版本下Scipy库中的L-BFGS-B优化函数实现。针对涉及到的机器学习模型，均采用贝叶斯优化[36]进行超参数优化。它是一种高效、鲁棒且具有理论支持的方法，能够更快地找到模型的最佳超参数组合，提高模型的性能和泛化能力[37]。
表1水文模型输入、输出变量概况
Tab.1 Description of input and output variables of the hydrologic models
2.4 评价指标
选取纳什系数（NSE）和均方根误差（RMSE）两种指标来评价水文模型在不同方案下的径流模拟效果，各指标的计算公式为：
NSE=1-Σt=1nQsim,t-Qobs,t2Σt=1nQobs,t-Q-obs,t2
(7)
RMSE=Σt=1nQsim,t-Qobs,t2n
(8)
式中，Qsim，t和Qobs，t分别表示t时刻模拟流量和实测流量；Q-obs，t表示实测流量的平均值；n表示时间序列长度；其中，NSE越接近1，RMSE越小，说明模型径流模拟效果越好，反之越差。
3 结果分析
3.1 参数率定
GR4J参数取值范围基于其物理概念并根据前期文献进行设定[38-39]，模型参数率定结果如表2所示。对于4种机器学习模型，采用贝叶斯优化方法对模型的待估计超参数进行调参，超参数取值范围参考前期文献设定，训练期4种模型的超参数取值范围相同[40-41]，验证期均采用训练期的最优超参数值，参数估计结果如表3所示。上述水文模型率定得到的模型参数最优值均在取值范围内，说明模型各参数取值均在合理范围内分布，可进一步用于流域径流模拟。
表2GR4J模型参数率定结果
Tab.2 Optimal values of the GR4J model's parameters
3.2 模型径流模拟评价
3.2.1 模型整体评价
本研究将数据集划分为预热期、训练期、验证期3部分，其中数据集时间跨度为2000年1月1日—2011年12月31日。数据集前1个月的数据（2000年1月1日—1月31日）用作模型预热，剩余数据的前80%用于模型训练，后20%用于模型验证。
表3机器学习模型超参数优化结果
Tab.3 Optimal values of hyperparameters of the machine learning models
表4和图3分别展示了5种模型在训练期和验证期（2000年2月1日—2011年12月31日）的模拟径流评价结果及径流模拟过程。总体而言，PIML-H3模型在所有模型中径流模拟结果最好，PIML-H1模型次之，而PIML-H2与LSTM模型的模拟结果相对较差。具体而言，3种PIML模型径流模拟效果均优于LSTM模型，其中验证期NSE平均提升10.6%；仅PIML-H1与PIML-H3模型径流模拟效果优于GR4J模型，验证期NSE平均提升4.2%，PIML-H2模型的改进效果并不显著，这说明基于物理概念公式确定目标变量的输入无法完全确保ML对其模拟精度的提高[42-43]，仅考虑土壤含水量作为补充输入对ML的改善效果有限。个别模型方案验证期精度高于训练期，主要由于采用贝叶斯优化机器学习超参数可能使模型正则化过多，从而导致模型在训练期和验证期模拟结果相差较大。此外，模型在训练期与验证期均方根误差均较大，主要是由于模型在高流量时的模拟值偏低。验证期模拟流量与实测流量绝对误差较大，主要由于验证期内2011年夏季出现的洪水洪量偏大，但训练期出现过与验证期内相同量级的洪水，因此，在进行参数率定时已将洪水造成的模拟影响考虑在内[3]。从总体上看，5种模型在汉江上游的径流模拟效果较为合理。
表4训练期与验证期水文模型径流模拟评价
Tab.4 Evaluation of runoff simulations obtained from the five hydrologic models during the calibration and validation periods
从5种模型2000年2月1日—2011年12月31日的流量模拟值与实测值的散点图（图4）可以看出，GR4J模型和PIML-H1、PIML-H3模型的散点图呈现出比其他模型更为紧密的分布，而LSTM和PIML-H2模型的散点图明显较为松散。在3个PIML模型中，PIML-H1（R2=0.83）表现最好，其次是PIML-H3（R2=0.78），最后是PIML-H2（R2=0.74）。尽管PIML-H3模型在主要评价指标上相较GR4J模型有所提升，但是R2却有所下降，这是由于模型PIML-H3模型比GR4J模型更复杂，模拟过程中更容易出现过拟合现象，导致数据泛化能力较差[44]。
图3训练期与验证期5种水文模型实测和模拟流量
Fig.3Observed and simulated flow by the five models during the calibration and validation periods
3.2.2 高水低水评价
图5展示了 5种模型实测流量和模拟流量的流量历时曲线（FDCs）。总体而言，除PIML-H1模型外，其他4种模型均在一定程度上低估了流量，尤其在高水部分更为显著。具体而言，PIML-H1、PIML-H2、PIML-H3模型以及LSTM模型在低水流量方面倾向于高估（图5b），而GR4J模型则倾向于低估。在模拟低水流量时，3种PIML模型效果均优于GR4J和LSTM模型，且PIML-H3模型效果最佳；而在模拟高水流量时，3种PIML模型均表现不佳（图5a），说明PIML模型在模拟低水流量事件中更占优势。
图4训练期与验证期5种模型模拟流量和实测流量散点图
Fig.4Scatterplot of simulated and observed flow of five models during the calibration and validation periods
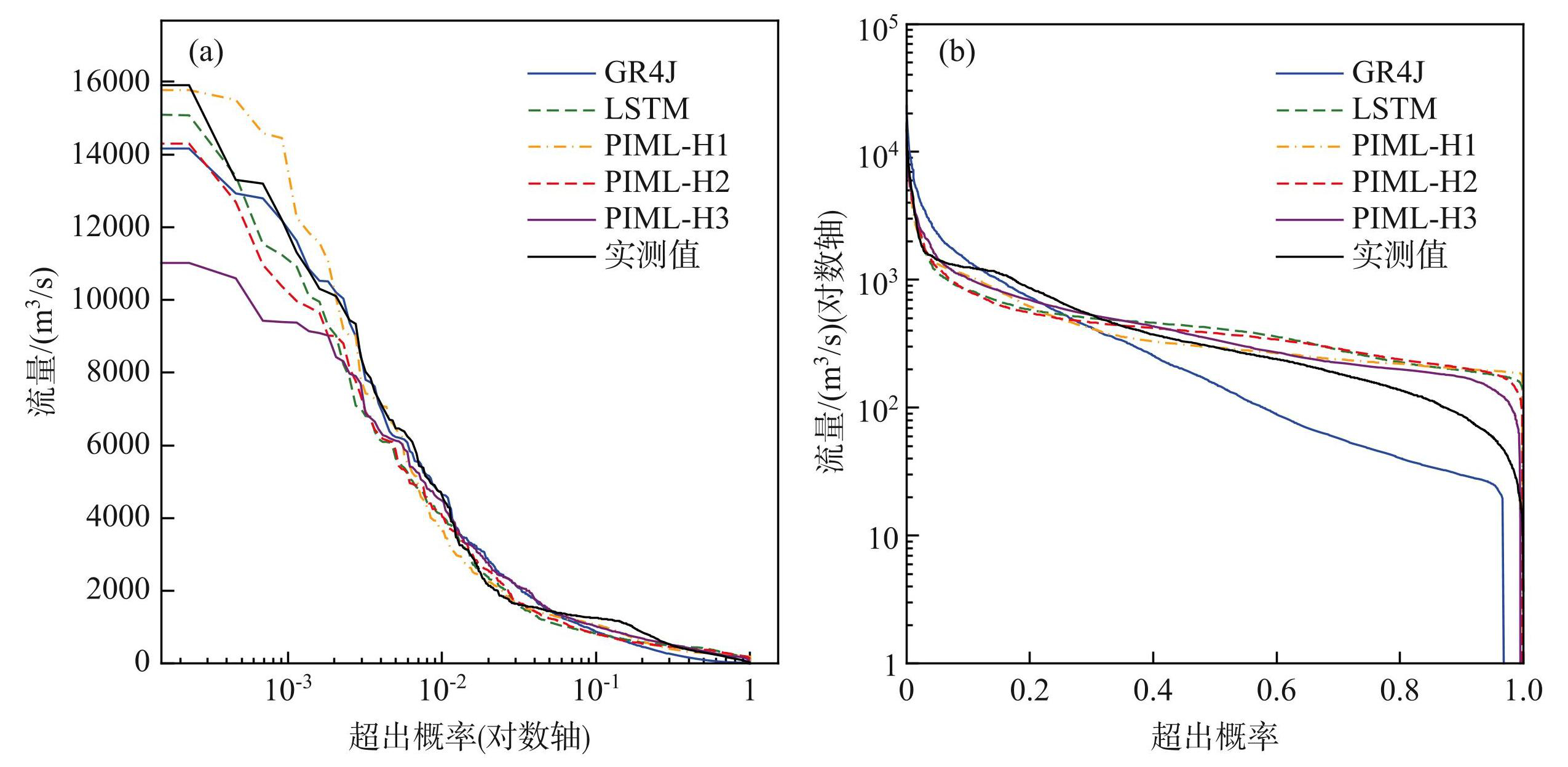
图5训练期与验证期5种模型实测流量和模拟流量的流量历时曲线
Fig.5Flow duration curves (FDCs) of observed and simulated flow of five models during the calibration and validation periods
图6呈现了2010年和2011年各模型的降水、流量变化情况。总体而言，除LSTM模型外，其他模型在2011年的预测中普遍表现为优于2010年。5种模型均未能准确捕捉2010年7月初—8月末的流量动态，其中GR4J模型、PIML-H1模型、PIML-H3模型在该阶段的模拟效果优于LSTM、PIML-H2，除GR4J和PIML-H3模型外，其他3种模型在2010年8月的高流量情况下均存在低估。GR4J模型在2011年8月高估了峰值流量，而LSTM和PIML-H2模型则存在低估。其中，PIML-H1和PIML-H3模型在2011年8月的模拟峰值流量与实测流量非常接近。2011年10月和11月期间，所有模型均呈现出流量低估的趋势，其中GR4J和PIML-H3模型相较于其他3个模型表现出的低估程度较小。相反，PIML-H2模型在该阶段表现出了异常的高估情况，这与该时期土壤含水量和短暂的小洪峰事件有关，较小的洪峰事件对初始土壤含水量更为敏感[45]。尽管PIML-H3同样涉及土壤含水量变量，但因其耦合过程受到多种因素制约，导致影响不明显。
图6验证期模型模拟流量和实测流量的对比（左列为2010年，右列为2011年）
Fig.6Comparison between simulated and observed flow during the validation period years (left and right columns represent the year of 2010 and 2011, respectively)
3.2.3 年际间变化趋势
图7给出了3种PIML模型在月尺度和多年平均月尺度上的径流模拟效果。从左列观察，3种PIML模型均在6—10月间有较大的径流深模拟量，在年份维度上，3种PIML模型均在2003—2005年以及2010—2011年有较大的径流深模拟量。从右列观察，PIML-H1和PIML-H3模型在整个数据集上的模拟效果明显优于PIML-H2模型。在月份维度上，表现较好的模拟结果集中在6—10月之间，说明在该时期PIML模型的模拟能力相对较强，且PIML-H3模型相较于PIML-H1模型受到的季节性变化影响更为明显，这与PIML-H3耦合过程中受到土壤含水量变化的影响有关[46]。在年份维度上，PIML-H1模型模拟较好的年份主要分布在2003—2011年之间，而PIML-H3模型模拟较好的年份则集中在2003—2005年以及2009—2011年，但3种模型模拟效果并未呈现出明显的差异。图7g展示了3种PIML模型模拟与实测的多年平均月径流深对比，总体上讲，PIML-H1模型模拟与实测的多年平均月径流深偏离程度最小，其次为PIML-H3，PIML-H2最差。具体而言，1—6月期间，PIML-H1与PIML-H3均在不同程度上低估了径流深，而PIML-H2则倾向于高估，6—8月以及10—11月之间，PIML-H3模拟值与实测值的平均差值最小，PIML-H2模型平均差值最大，说明同时考虑中间变量和参数反馈因素在短时间内径流急剧变化下的径流模拟效果较好。
图7训练期和验证期3种PIML模型月径流深热图及多年平均月径流深折线图 （图a~b、c~d、e~f分别代表PIML-H1、PIML-H2、PIML-H3 3种模型的月径流深热图）
Fig.7Thermal plots illustrating monthly runoff depth during the calibration and validation periods for three PIML models (PIML-H1 (a-b) , PIML-H2 (c-d) and PIML-H3 (e-f) ) along with line graphs depicting the multi-year average monthly runoff depth）
图8为5种模型在训练期和验证期各季节的径流模拟效果泰勒图，图中径向线反映线性相关系数，水平轴和垂直轴表示标准差，虚线则表示均方根标准差（RMSD）。本研究按照3—5月为春季、6—8月为夏季、9—11月为秋季、12月—次年2月为冬季来划分四季[47]。总体而言，在春、夏季阶段，相较于PIML-H2和LSTM模型，GR4J、PIML-H1、PIML-H3模型的相关性较高，但标准差和RMSD较低；3种模型中，GR4J模型呈现出最低的标准差和均方根标准差，而PIML-H1模型则展现出最大的线性相关系数。5种模型在秋季的径流模拟效果较好，而在春季和冬季则有所下降。具体而言，除LSTM、PIML-H2模型外，其余3种模型在夏季的模拟效果均较春季有所提升，从夏季到秋季，5种模型的线性相关系数均有所升高，且标准差下降，整体模拟效果提升。从秋季到冬季，5种模型的标准差均有较大幅度增加，模型的模拟效果整体下降。
图8春（a）、夏（b）、秋（c）、冬（d）季训练期与验证期5种模型的径流模拟精度泰勒图
Fig.8Performance of Taylor diagrams for five models during calibration and validation periods over spring (a) , summer (b) , autumn (c) and winter (d)
4 结论
本研究基于GR4J和LSTM模型构建了PIML模型，并分别设置了考虑参数反馈、考虑中间变量和两者同时考虑的3种方案（依次简称为H1、H2、H3），探讨了GR4J与LSTM耦合过程中物理模型参数反馈机制以及考虑土壤含水量作为中间变量对PIML模型构建的影响，其主要结论如下：
1）3种PIML模型径流模拟效果均优于LSTM模型，其中验证期平均NSE平均提升10.6%，PIML-H1与PIML-H3模型径流模拟效果优于GR4J模型，验证期NSE平均提升4.2%，PIML-H3模型在3种PIML模型中表现最佳，说明基于LSTM和GR4J模型构建的PIML模型对径流模拟效果有所改善，同时考虑中间变量和参数反馈因素对径流模拟效果改善最佳。
2）除PIML-H1模型外，其他4种模型均在一定程度上低估了流量，尤其在高水部分更为显著。在模拟低水流量时，3种PIML模型的模拟效果均优于GR4J和LSTM模型，PIML-H3模型效果最佳。而对于高水流量，3种PIML模型均表现不佳，可见PIML模型往往在模拟低水流量事件中更占优势。
3）3种PIML模型在训练和验证期间模拟结果均出现较强的季节性变化特征，并在6—10月均表现出较好的模拟效果。PIML-H2和PIML-H3模型相较于PIML-H1模型受到的季节性变化影响更为明显，可见PIML模型模拟结果的季节性变化与耦合过程中土壤含水量变化有关。
总之，同时考虑参数反馈以及土壤含水量作为中间变量对PIML模型耦合的影响，在一定程度上能提升径流模拟效果。为了充分体现中间变量和参数反馈的必要性，在未来研究中可考虑更合适的中间变量以及参数反馈架构来提高径流模拟精度。另外，如何尽可能减小机器学习模型预测水文模型参数过程中的不确定性、探究不同中间变量对PIML耦合结果的影响，还有待深入研究。
图1汉江上游流域地理位置及气象站、水文站分布
Fig.1Location of the upper Han River Basin and the distribution of meteorological and hydrological stations
图23种PIML模型方案流程
Fig.2The architectural framework of three scenarios of PIML model
图3训练期与验证期5种水文模型实测和模拟流量
Fig.3Observed and simulated flow by the five models during the calibration and validation periods
图4训练期与验证期5种模型模拟流量和实测流量散点图
Fig.4Scatterplot of simulated and observed flow of five models during the calibration and validation periods
图5训练期与验证期5种模型实测流量和模拟流量的流量历时曲线
Fig.5Flow duration curves (FDCs) of observed and simulated flow of five models during the calibration and validation periods
图6验证期模型模拟流量和实测流量的对比（左列为2010年，右列为2011年）
Fig.6Comparison between simulated and observed flow during the validation period years (left and right columns represent the year of 2010 and 2011, respectively)
图7训练期和验证期3种PIML模型月径流深热图及多年平均月径流深折线图 （图a~b、c~d、e~f分别代表PIML-H1、PIML-H2、PIML-H3 3种模型的月径流深热图）
Fig.7Thermal plots illustrating monthly runoff depth during the calibration and validation periods for three PIML models (PIML-H1 (a-b) , PIML-H2 (c-d) and PIML-H3 (e-f) ) along with line graphs depicting the multi-year average monthly runoff depth）
图8春（a）、夏（b）、秋（c）、冬（d）季训练期与验证期5种模型的径流模拟精度泰勒图
Fig.8Performance of Taylor diagrams for five models during calibration and validation periods over spring (a) , summer (b) , autumn (c) and winter (d)
表1水文模型输入、输出变量概况
表2GR4J模型参数率定结果
表3机器学习模型超参数优化结果
表4训练期与验证期水文模型径流模拟评价
Qiao PW, Wang S, Li JB et al. Process,influencing factors,and simulation of the lateral transport of heavy metals in surface runoff in a mining area driven by rainfall: A review. Science of the Total Environment,2023,857(Pt1):159119. DOI:10.1016/j.scitotenv.2022.159119.
Luo S, Xu YP, Wang Q et al. The evolution of annual maximum daily runoff and its influencing factors under the back-ground of urbanization: An example of Qinhuai River Basin in the lower reaches of the Yangtze River. J Lake Sci,2023,35(6):2123-2132. DOI:10.18307/2023.0642.[罗爽, 许有鹏, 王强等. 城市化背景下年最大日径流演变及影响因素研究. 湖泊科学,2023,35(6):2123-2132.]
Wang WG, Zou JC, Deng C. Comparison of data assimilation based approach for daily streamflow simulation under multiple scenarios in Ganjiang River Basin. J Lake Sci,2023,35(3):1047-1056. DOI:10.18307/2023.0323.[王卫光, 邹佳成, 邓超. 赣江流域多种数据同化方案的径流模拟比较. 湖泊科学,2023,35(3):1047-1056.]
Fan HX, He HD, Xu LG et al. Simulation and attribution analysis based on the long-short-term-memory network for detecting the dominant cause of runoff variation in the Lake Poyang Basin. J Lake Sci,2021,33(3):866-878. DOI:10.18307/2021.0319.[范宏翔, 何菡丹, 徐力刚等. 基于长短记忆模型的鄱阳湖流域径流模拟及其演变的归因分析. 湖泊科学,2021,33(3):866-878.]
Zhao LX, Guo ZL, Nie XF et al. Effects of extreme rainfall events on runoff and sediment in the southern red soil area: A long series analysis based on the Upper Lianjiang River of Ganjiang River(1984-2020). J Lake Sci,2023,35(6):2133-2143. DOI:10.18307/2023.0643.[赵利祥, 郭忠录, 聂小飞等. 极端降雨事件对南方红壤区径流和输沙的影响——基于赣江支流濂江上游流域的长序列分析(1984—2020年). 湖泊科学,2023,35(6):2133-2143.]
Guan TS, Bao ZX, He RM et al. Uncertainties of model parameters regionalization in ungauged basins. Advances in Water Science,2023,34(5):660-672.[关铁生, 鲍振鑫, 贺瑞敏等. 无资料地区水文模型参数移植不确定性分析. 水科学进展,2023,34(5):660-672.]
Devia GK, Ganasri BP, Dwarakish GS. A review on hydrological models. Aquatic Procedia,2015,4:1001-1007. DOI:10.1016/j.aqpro.2015.02.126.
Yaseen ZM, El-shafie A, Jaafar O et al. Artificial intelligence based models for stream-flow forecasting:2000-2015. Journal of Hydrology,2015,530:829-844. DOI:10.1016/j.jhydrol.2015.10.038.
Lin GF, Chou YC, Wu MC. Typhoon flood forecasting using integrated two-stage Support Vector Machine approach. Journal of Hydrology,2013,486:334-342. DOI:10.1016/j.jhydrol.2013.02.012.
Xiang ZR, Yan J, Demir I. A rainfall-runoff model with LSTM-based sequence-to-sequence learning. Water Resources Research,2020,56(1):e2019WR025326. DOI:10.1029/2019WR025326.
Kratzert F, Klotz D, Brenner C et al. Rainfall-runoff modelling using Long Short-Term Memory(LSTM)networks. Hydrology and Earth System Sciences,2018,22(11):6005-6022. DOI:10.5194/hess-22-6005-2018.
Gao S, Huang YF, Zhang S et al. Short-term runoff prediction with GRU and LSTM networks without requiring time step optimization during sample generation. Journal of Hydrology,2020,589:125188. DOI:10.1016/j.jhydrol.2020.125188.
Beven K. Deep learning,hydrological processes and the uniqueness of place. Hydrological Processes,2020,34(16):3608-3613. DOI:10.1002/hyp.13805.
Gilpin LH, Bau D, Yuan BZ et al. Explaining explanations: An overview of interpretability of machine learning.2018 IEEE 5th International Conference on Data Science and Advanced Analytics(DSAA). Turin, Italy. IEEE,2018:80-89. DOI:10.1109/DSAA.2018.00018.
Yang SY, Yang DW, Chen JS et al. A physical process and machine learning combined hydrological model for daily streamflow simulations of large watersheds with limited observation data. Journal of Hydrology,2020,590:125206. DOI:10.1016/j.jhydrol.2020.125206.
Nourani V. An Emotional ANN(EANN)approach to modeling rainfall-runoff process. Journal of Hydrology,2017,544:267-277. DOI:10.1016/j.jhydrol.2016.11.033.
Jiang SJ, Zheng Y, Solomatine D. Improving AI system awareness of geoscience knowledge: Symbiotic integration of physical approaches and deep learning. Geophysical Research Letters,2020,47(13):e2020GL088229. DOI:10.1029/2020GL088229.
Kashinath K, Mustafa M, Albert A et al. Physics-informed machine learning: Case studies for weather and climate modelling. Philosophical Transactions Series A, Mathematical, Physical,and Engineering Sciences,2021,379(2194):20200093. DOI:10.1098/rsta.2020.0093.
Humphrey GB, Gibbs MS, Dandy GC et al. A hybrid approach to monthly streamflow forecasting: Integrating hydrological model outputs into a Bayesian artificial neural network. Journal of Hydrology,2016,540:623-640. DOI:10.1016/j.jhydrol.2016.06.026.
Okkan U, Ersoy ZB, Ali Kumanlioglu A et al. Embedding machine learning techniques into a conceptual model to improve monthly runoff simulation: A nested hybrid rainfall-runoff modeling. Journal of Hydrology,2021,598:126433. DOI:10.1016/j.jhydrol.2021.126433.
Badrzadeh H, Sarukkalige R, Jayawardena AW. Hourly runoff forecasting for flood risk management: Application of various computational intelligence models. Journal of Hydrology,2015,529:1633-1643. DOI:10.1016/j.jhydrol.2015.07.057.
Yu Q, Jiang LG, Wang YJ et al. Enhancing streamflow simulation using hybridized machine learning models in a semi-arid basin of the Chinese loess Plateau. Journal of Hydrology,2023,617:129115. DOI:10.1016/j.jhydrol.2023.129115.
Bian LK, Qin XE, Zhang CL et al. Application,interpretability and prediction of machine learning method combined with LSTM and LightGBM-A case study for runoff simulation in an arid area. Journal of Hydrology,2023,625:130091. DOI:10.1016/j.jhydrol.2023.130091.
Deng C, Chen CY, Yin X et al. Catchment runoff simulation by coupling data assimilation and machine learning methods. Advances in Water Science,2023,34(6):839-849.[邓超, 陈春宇, 尹鑫等. 融合数据同化与机器学习的流域径流模拟方法. 水科学进展,2023,34(6):839-849.]
Bhasme P, Vagadiya J, Bhatia U. Enhancing predictive skills in physically-consistent way: Physics Informed Machine Learning for hydrological processes. Journal of Hydrology,2022,615:128618. DOI:10.1016/j.jhydrol.2022.128618.
Pan X, Qin CC. Study on temporal and spatial evolution law of precipitation in Hanjiang River Basin. Express Water Resources & Hydropower Information,2023,(6):333-343.[潘鑫, 秦创创. 汉江流域降水时空演变特征研究. 水利水电快报,2023,(6):333-343.]
Wang D, Wu DD, Xie XB et al. Study on spatio-temporal variation of runoff in flood season in Hanjiang River Basin. Pearl River,2020,41(4):30-39.[王栋, 吴栋栋, 解效白等. 汉江流域汛期径流时空变化特征研究. 人民珠江,2020,41(4):30-39.]
Liu YW, Li JK, Ding Q et al. Characteristic analysis and prediction of rainfall and runoff in Ankang section of Hanjiang River Basin. Pearl River,2021,42(6):59-69.[刘易文, 李家科, 丁强等. 汉江流域安康段降雨径流特征分析及预测. 人民珠江,2021,42(6):59-69.]
Allen RG, Pereira LS, Raes D et al. Crop evapotranspiration: Guidelines for computing crop requirements. FAO Irrigation and Drainage Paper,1998:56.
Perrin C, Michel C, Andréassian V. Improvement of a parsimonious model for streamflow simulation. Journal of Hydrology,2003,279(1/2/3/4):275-289. DOI:10.1016/s0022-1694(03)00225-7.
Kunnath-Poovakka A, Eldho TI. A comparative study of conceptual rainfall-runoff models GR4J, AWBM and Sacramento at catchments in the upper Godavari River Basin, India. Journal of Earth System Science,2019,128(2):33. DOI:10.1007/s12040-018-1055-8.
Wang HY, Guo SL, Wang J et al. Comparative study of GR4J and Xinanjiang models in humid area. Journal of Water Resources Research,2021,(1):11-20.[王何予, 郭生练, 王俊等. GR4J与新安江模型在湿润地区比较研究. 水资源研究,2021,(1):11-20.]
Hochreiter S, Schmidhuber J. Long short-term memory. Neural Computation,1997,9(8):1735-1780. DOI:10.1162/neco.1997.9.8.1735.
Sherstinsky A. Fundamentals of Recurrent Neural Network(RNN)and Long Short-Term Memory(LSTM)network. Physica D: Nonlinear Phenomena,2020,404:132306. DOI:10.1016/j.physd.2019.132306.
Alhirmizy S, Qader B. Multivariate Time Series Forecasting with LSTM for Madrid, Spain pollution.2019 International Conference on Computing and Information Science and Technology and Their Applications(ICCISTA). Kirkuk, Iraq. IEEE,2019:1-5. DOI:10.1109/ICCISTA.2019.8830667.
Berkenkamp F, Krause A, Schoellig AP. Bayesian optimization with safety constraints: Safe and automatic parameter tuning in robotics. Machine Learning,2023,112(10):3713-3747. DOI:10.1007/s10994-021-06019-1.
Joy TT, Rana ST, Gupta S et al. Fast hyperparameter tuning using Bayesian optimization with directional derivatives. Knowledge-Based Systems,2020,205:106247. DOI:10.1016/j.knosys.2020.106247.
Deng PX, Wang YT, Hu QF et al. Application of GR4J in daily runoff simulation for Ganjiang River Basin. Journal of China Hydrology,2014,34(2):60-65.[邓鹏鑫, 王银堂, 胡庆芳等. GR4J模型在赣江流域日径流模拟中的应用. 水文,2014,34(2):60-65.]
Wei XJ, Guo SL, Xiong LH. Improving efficiency of hydrological prediction based on meteorological classification: A case study of GR4J model. Water,2021,13(18):2546. DOI:10.3390/w13182546.
Habtemariam ET, Kekeba K, Martínez-Ballesteros M et al. A Bayesian optimization-based LSTM model for wind power forecasting in the Adama district, Ethiopia. Energies,2023,16(5):2317. DOI:10.3390/en16052317.
Skomski E, Lee JY, Kim W et al. Sequence-to-sequence neural networks for short-term electrical load forecasting in commercial office buildings. Energy and Buildings,2020,226:110350. DOI:10.1016/j.enbuild.2020.110350.
Wang S, Peng H, Hu Q et al. Analysis of runoff generation driving factors based on hydrological model and interpretable machine learning method. Journal of Hydrology: Regional Studies,2022,42:101139. DOI:10.1016/j.ejrh.2022.101139.
Prendin F, Pavan J, Cappon G et al. The importance of interpreting machine learning models for blood glucose prediction in diabetes: An analysis using SHAP. Scientific Reports,2023,13:16865. DOI:10.1038/s41598-023-44155-x.
Chollet Ramampiandra E, Scheidegger A, Wydler J et al. A comparison of machine learning and statistical species distribution models: Quantifying overfitting supports model interpretation. Ecological Modelling,2023,481:110353. DOI:10.1016/j.ecolmodel.2023.110353.
Grillakis MG, Koutroulis AG, Komma J et al. Initial soil moisture effects on flash flood generation—A comparison between basins of contrasting hydro-climatic conditions. Journal of Hydrology,2016,541:206-217. DOI:10.1016/j.jhydrol.2016.03.007.
Wang S, Fu BJ, Gao GY et al. Soil moisture and evapotranspiration of different land cover types in the Loess Plateau, China. Hydrology and Earth System Sciences,2012,16(8):2883-2892. DOI:10.5194/hess-16-2883-2012.
Xiong Y, Zhou JZ, Sun N et al. Monthly runoff prediction based on self-adaptive variational mode decomposition and long short-term memory network. Journal of Hydraulic Engineering,2023,54(2):172-183,198.[熊怡, 周建中, 孙娜等. 基于自适应变分模态分解和长短期记忆网络的月径流预报. 水利学报,2023,54(2):172-183,198.]